题目内容
16.已知复数z=-2+i,则复数$\frac{z+3}{\overline z+2}$的模为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 把z=-2+i代入$\frac{z+3}{\overline z+2}$,利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.
解答 解:∵z=-2+i,
∴$\frac{z+3}{\overline z+2}=\frac{-2+i+3}{-2-i+2}=\frac{1+i}{-i}=-1+i$,
则复数$\frac{z+3}{\overline z+2}$的模$\sqrt{{{(-1)}^2}+{1^2}}=\sqrt{2}$,
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了共轭复数的概念,考查复数模的求法,是基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
1.已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn是数列{an}的前n项和,则$\frac{{2{S_n}+8}}{{{a_n}+3}}({n∈{N^*}})$的最小值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{8}{3}$ | C. | $2\sqrt{5}-2$ | D. | 3 |
6.过抛物线y2=4x焦点F的直线交抛物线于A,B两点,交其准线于点C,且A,C位于x轴同侧,若|AC|=2|AF|,则直线AB的斜率为( )
| A. | ±1 | B. | $±\sqrt{3}$ | C. | ±2 | D. | $±\sqrt{5}$ |
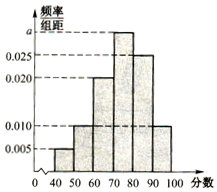 为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.