题目内容
 如图,在四边形ABCD中,∠DAB=90°,∠ADC=30°,AB=AD=4,CD=2.将四边形ABCD绕AD旋转一周,则所成几何体的体积为
如图,在四边形ABCD中,∠DAB=90°,∠ADC=30°,AB=AD=4,CD=2.将四边形ABCD绕AD旋转一周,则所成几何体的体积为(28-
)π
20
| ||
| 3 |
(28-
)π
20
| ||
| 3 |
(台体的体积公式V=
| 1 |
| 3 |
| S1S2 |
分析:先过C作AD的垂线求得圆锥的旋转半径与高,再根据圆锥与圆台的体积公式计算即可.
解答: 解:过C作CO垂直于AD,垂足为O,
解:过C作CO垂直于AD,垂足为O,
将四边形ABCD绕AD旋转一周所成几何体为一个圆锥与一个圆台的组合体,
在△OCD中,∠ADC=30°,CD=2,∴OC=1,OD=
∴V圆锥=
×π×
=
π;
V圆台=
π×(1+4+16)×(4-
)=28π-7
π.
V=V圆锥+V圆台=28π-
π.
故答案是(28-
)π.
 解:过C作CO垂直于AD,垂足为O,
解:过C作CO垂直于AD,垂足为O,将四边形ABCD绕AD旋转一周所成几何体为一个圆锥与一个圆台的组合体,
在△OCD中,∠ADC=30°,CD=2,∴OC=1,OD=
| 3 |
∴V圆锥=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
V圆台=
| 1 |
| 3 |
| 3 |
| 3 |
V=V圆锥+V圆台=28π-
20
| ||
| 3 |
故答案是(28-
20
| ||
| 3 |
点评:本题考查旋转体的体积.V圆锥=
πr2h;V圆台=
π(r2+rR+R2)h.
| 1 |
| 3 |
| 1 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四边形ABCD中,△ABC为边长等于
如图,在四边形ABCD中,△ABC为边长等于 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC= 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=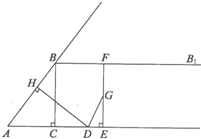 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,