题目内容
在一条长为2的线段上任取两点,则这两点到线段中点的距离的平方和大于1的概率为
.
| 4-π |
| 4 |
| 4-π |
| 4 |
分析:设取出的两点到中点的距离为x、y,有0≤x≤1,0≤y≤1,可得其表示的区域为边长为1的正方形,进而可得其面积,若这两点到线段中点的距离的平方和大于1,即x2+y2>1,可得其表示的图形及面积,由几何概型公式计算可得答案.
解答: 解:设取出的两点到中点的距离为x、y,有0≤x≤1,0≤y≤1,其表示的区域为边长为1的正方形,如图,其面积为1,
解:设取出的两点到中点的距离为x、y,有0≤x≤1,0≤y≤1,其表示的区域为边长为1的正方形,如图,其面积为1,
若这两点到线段中点的距离的平方和大于1,即x2+y2>1,如图阴影,其面积为
•π•12,
由几何概型可得,这两点到线段中点的距离的平方和大于1的概率为
=
;
故答案为
.
 解:设取出的两点到中点的距离为x、y,有0≤x≤1,0≤y≤1,其表示的区域为边长为1的正方形,如图,其面积为1,
解:设取出的两点到中点的距离为x、y,有0≤x≤1,0≤y≤1,其表示的区域为边长为1的正方形,如图,其面积为1,若这两点到线段中点的距离的平方和大于1,即x2+y2>1,如图阴影,其面积为
| 1 |
| 4 |
由几何概型可得,这两点到线段中点的距离的平方和大于1的概率为
1-
| ||
| 1 |
| 4-π |
| 4 |
故答案为
| 4-π |
| 4 |
点评:本题考查几何概型的计算,注意本题要先设出距离,得到关于x、y的二元方程组,转化为几何概型的问题.

练习册系列答案
相关题目
 已知两点P(-2,2),Q(0,2)以及一条直线:L:y=x,设长为
已知两点P(-2,2),Q(0,2)以及一条直线:L:y=x,设长为 及点
及点 ,在
,在 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 。
。 到线段
到线段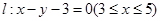 的距离
的距离 所表示图形的面积;
所表示图形的面积; 距离相等的点的集合
距离相等的点的集合 ,其中
,其中 ,
, 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。 。
。 。
。 。
。