题目内容
已知一条长为6的线段两端点A、B分别在x、y轴上滑动,点M在线段AB上,且AM∶MB=1∶2,求动点M的轨迹方程.
答案:
解析:
解析:
|
解:设A(a,0),B(0,b),M(x,y). ∵|AB|=6.∴a2+b2=36. ① 又∵AM∶MB=1∶2,∴M分 由定比分点坐标公式知: 即 分析:所求动点M随A、B两点的变化而变化,而由A、B两点的定长6可建立出坐标关系.由AM∶MB=1∶2可将A、B坐标用M(x,y)中x、y表示.故可采用代入法求解. |

练习册系列答案
相关题目
 代入①或得(
代入①或得( 及点
及点 ,在
,在 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 。
。 到线段
到线段 的距离
的距离 所表示图形的面积;
所表示图形的面积; 距离相等的点的集合
距离相等的点的集合 ,其中
,其中 ,
, 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。 。
。 。
。 。
。 及点
及点 ,在
,在 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 。
。 到线段
到线段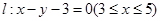 的距离
的距离 所表示图形的面积;
所表示图形的面积; 距离相等的点的集合
距离相等的点的集合 ,其中
,其中 ,
, 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。 。
。 。
。 。
。