Question

【题目】已知椭圆 的离心率为 ，且过点 .
（1）求椭圆 的方程；
（2）设不过原点 的直线 与椭圆 交于 两点，直线 的斜率分别为 ，满足 ，试问：当 变化时， 是否为定值？若是，求出此定值，并证明你的结论；若不是，请说明理由.

Answer 1

【答案】
（1）解：依题意可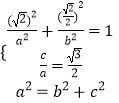得 解得 .
椭圆 的方程是
（2）解：当 变化时， 为定值，证明如下：
由 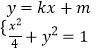得， .
设 ， ，则 ， （*）
∵直线 的斜率依次为 ，且 ，
∴ ，得 ，
将（*）代入得： ，
经检验满足
m 2 为定值
【解析】（1）由条件列出关于a,b,c的方程组求a,b,c得到椭圆方程;
（2）将直线方程代入椭圆方程消去y得到关于x的一元二次方程，用韦达定理表示出两根和与两根积，代入条件中求出m2为定值.