题目内容
13.已知抛物线的顶点在原点,焦点在x轴上,△ABC三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点,若BC边所在直线的方程为4x+y-20=0,则抛物线方程为y2=16x.分析 设抛物线的方程为y2=2px,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合直线l与抛物线相交于两个不同的点得到根的判别式大于0,结合根与系数的关系利用重心公式即可求得p值,从而解决问题.
解答 解:设抛物线的方程为y2=2px.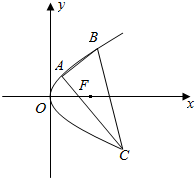
由$\left\{\begin{array}{l}4x+y-20=0\\{y}^{2}=2px\end{array}\right.$可得2y2+py-20p=0.
由△>0,有p>0,或p<-160.
设B(x1,y1),C(x2,y2),则y1+y2=-$\frac{p}{2}$,
∴x1+x2=(5-$\frac{{y}_{1}}{4}$)+(5-$\frac{{y}_{2}}{4}$)=10-$\frac{1}{4}$(y1+y2)=10+$\frac{p}{8}$,
设A(x3,y3),由△ABC的重心为F($\frac{p}{2}$,0),则$\frac{{x}_{1}+{x}_{2}+{x}_{3}}{3}$=$\frac{p}{2}$,$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$=0,
∴x3=$\frac{11p}{8}$-10,y3=$\frac{p}{2}$.
∵点A在抛物线上,
∴($\frac{p}{2}$)2=2p($\frac{11p}{8}$-10),
∴p=8.
∴抛物线的方程为y2=16x,
故答案为:y2=16x
点评 本题考查的知识点是抛物线的标准方程,直线与圆锥曲线的位置关系,重心坐标公式,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.为了宣传2015年10月在贵阳举行的“世界众筹大会”,“世界众筹大会”筹委会举办了“大众创业、万众创新”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如图所示:
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 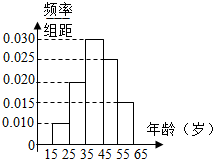 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65] | 3 | 0.2 |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.
5.若点A(2,-4),点B(-2,-5),则向量$\overrightarrow{AB}$的坐标为( )
| A. | (-4,-1) | B. | (4,1) | C. | (0,-9) | D. | (-2,-5) |