题目内容
如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若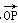 =xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
=xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
(1) 若P点斜坐标为(2,-2),求P到O的距离|PO|;
(2) 求以O为圆心,1为半径的圆在斜坐标系xOy中的方程.
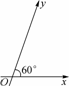
解:(1) ∵P点斜坐标为(2,-2),
∴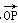 =2e1-2e2.
=2e1-2e2.
∴|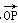 |2=(2e1-2e2)2=8-8e1·e2=8-8×cos60°=4.
|2=(2e1-2e2)2=8-8e1·e2=8-8×cos60°=4.
∴| |=2,即|OP|=2.
|=2,即|OP|=2.
(2) 设圆上动点M的斜坐标为(x,y),则 =xe1+ye2.
=xe1+ye2.
∴(xe1+ye2)2=1.
∴x2+y2+2xye1·e2=1.∴x2+y2+xy=1.
故所求方程为x2+y2+xy=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 的最大值和最小正周期;
的最大值和最小正周期;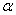 为锐角,且
为锐角,且 ,求
,求 的值.
的值.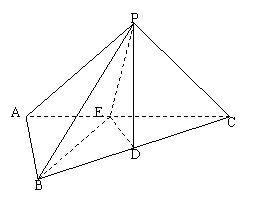
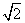 .求动点M的轨迹方程,并说明它表示什么.
.求动点M的轨迹方程,并说明它表示什么.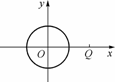
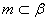 ,则α⊥β
,则α⊥β 中,
中, ,
, 分别是
分别是 及
及 的中点,
的中点, 是
是 的中点,沿
的中点,沿 ,
, 及
及 ,
, ,
, 折起使
折起使 ,
, ,
, 三点重合,重合后的点记作
三点重合,重合后的点记作 ,那么在四面体
,那么在四面体 中必有( )
中必有( ) 面
面 B.
B. 面
面 C.
C. 面
面 面
面 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( ) 则
则 B.若
B.若 则
则
 则
则 D.若
D.若 则
则
 等于:( )
等于:( ) C.
C. D.
D.