题目内容
【题目】已知函数![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值
的值
(2)当![]() 且
且![]() 时,求证:
时,求证: ![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:先从切线方程中找到![]() 的值,构建方程组得参数
的值,构建方程组得参数![]() 的值.(2)中的不等式较为麻烦,可以根据(1)的提示,考虑
的值.(2)中的不等式较为麻烦,可以根据(1)的提示,考虑![]() 与
与![]() 之间的关系,然后再考虑
之间的关系,然后再考虑![]() 与
与![]() 的关系,两者均需通过合理变形构建新函数并利用导数去考虑.
的关系,两者均需通过合理变形构建新函数并利用导数去考虑.
解析:(1)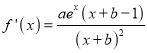 ,因在
,因在![]() 处的切线为
处的切线为![]() ,故
,故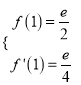 ,解得
,解得![]() .
.
(2)![]() ,令
,令![]() ,则
,则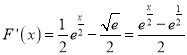 .
.
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 是减函数;
是减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 是增函数;
是增函数;
所以![]() ,故
,故![]() 在
在![]() 上恒成立,也就是
上恒成立,也就是![]() 在
在![]() 上恒成立,整理得到
上恒成立,整理得到![]() ,
, ![]() 恒成立.故
恒成立.故![]() 当且仅当
当且仅当![]() 等号成立.所以当
等号成立.所以当![]() 且
且![]() 时,
时, ![]() .
.
令![]() ,
, 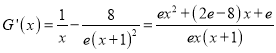 ,
, ![]() ,故
,故![]() 在
在![]() 上总成立,
上总成立, ![]() 在
在![]() 上为增函数,又
上为增函数,又![]() ,所以
,所以
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上恒成立,
上恒成立, ![]() ,故
,故 ![]() ;
;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上恒成立,
上恒成立, ![]() ,故也有
,故也有![]() ;
;
综上当![]() 时
时![]() .
.

练习册系列答案
相关题目
