题目内容
在△ABC中，a=2
，b=2
，∠B=45°，则∠A=（ ）
| 3 |
| 2 |
| A、30°或120° |
| B、60° |
| C、60°或120° |
| D、30° |
考点：正弦定理
专题：解三角形
分析：由题意和正弦定理求出sinA的值，再由内角的范围和边角关系求出角A的值．
解答：
解：由题意知，a=2
，b=2
，∠B=45°，
由正弦定理得，
=
，
则sinA=
=
=
，
因为0＜A＜180°，且a＞b，所以A=60°或120°，
故选：C．
| 3 |
| 2 |
由正弦定理得，
| a |
| sinA |
| b |
| sinB |
则sinA=
| asinB |
| b |
2
| ||||||
2
|
| ||
| 2 |
因为0＜A＜180°，且a＞b，所以A=60°或120°，
故选：C．
点评：本题考查正弦定理，内角的范围，以及边角关系，属于中档题和易错题．
练习册系列答案
相关题目
如图所示的数阵叫“莱布尼兹调和三角形”，他们是由整数的倒数组成的，第n行有n个数且两端的数均为
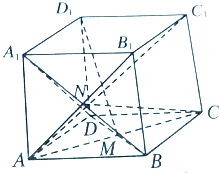如图，在正方形ABCD-A1B1C1D1中，M，N分别为正方形ABCD和AA1B1B的重心．
如图，已知PA⊥矩形ABCD所在的平面，E，F分别为AB，PC的中点，