题目内容
已知数列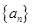 的前
的前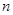 项和
项和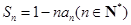 .
.
(1)计算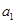 ,
,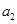 ,
,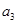 ,
,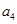 ;
;
(2)猜想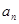 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论
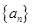 的前
的前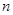 项和
项和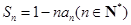 .
.(1)计算
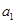 ,
,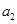 ,
,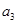 ,
,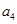 ;
;(2)猜想
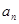 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论(1)依题设可得 ,
, ,
, ,
, ;
;
(2)猜想: .
.
证明:①当 时,猜想显然成立.
时,猜想显然成立.
②假设 时,猜想成立,
时,猜想成立,
即 .那么,当
.那么,当 时,
时, ,即
,即 .
.
又 ,所以
,所以 ,
,
从而 .即
.即 时,猜想也成立.
时,猜想也成立.
故由①和②,可知猜想成立.
 ,
, ,
, ,
, ;
;(2)猜想:
 .
.证明:①当
 时,猜想显然成立.
时,猜想显然成立.②假设
 时,猜想成立,
时,猜想成立,即
 .那么,当
.那么,当 时,
时, ,即
,即 .
.又
 ,所以
,所以 ,
,从而
 .即
.即 时,猜想也成立.
时,猜想也成立.故由①和②,可知猜想成立.
(1)分别令n=1,2,3,4,依次求出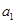 ,
,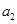 ,
,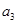 ,
,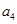 的值.
的值.
(2)再用数学归纳法证明时要按两个步骤进行,缺一不可
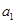 ,
,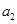 ,
,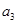 ,
,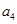 的值.
的值.(2)再用数学归纳法证明时要按两个步骤进行,缺一不可

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
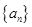 中,已知
中,已知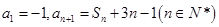 。
。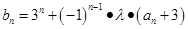 (
(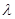 为非零常数),问是否存在整数
为非零常数),问是否存在整数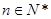 都有
都有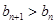 ?若存在,求出
?若存在,求出 }的前n项和
}的前n项和 满足:
满足: }的前n项和为
}的前n项和为 ,公比为
,公比为 ,且
,且 =
= +2
+2 .
. }的前n项和为
}的前n项和为 ,求证:
,求证: ≤
≤ .
.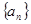 的前n项和
的前n项和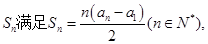 且
且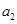 =2.
=2.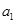 的值,并证明:当n>2时有
的值,并证明:当n>2时有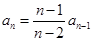 ;
;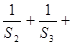 …
…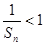 .
. 的前n项和为
的前n项和为 ,且满足:
,且满足:
 ;
;
 求数列
求数列
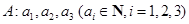 ,定义“
,定义“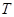 变换”:
变换”: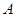 变换成数列
变换成数列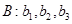 ,其中
,其中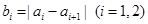 ,且
,且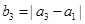 .这种“
.这种“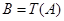 .继续对数列
.继续对数列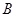 进行“
进行“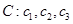 ,依此类推,当得到的数列各项均为
,依此类推,当得到的数列各项均为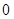 时变换结束.
时变换结束.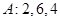 经过不断的“
经过不断的“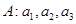 ,
,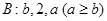 ,且
,且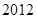 .
.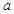 ,
,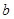 ;
;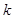 次“
次“ }是首项为23,公差为整数的等差数列,且前6项为正,从第7项开始变为负的,回答下列各问:(1)求此等差数列的公差d;(2)设前n项和为
}是首项为23,公差为整数的等差数列,且前6项为正,从第7项开始变为负的,回答下列各问:(1)求此等差数列的公差d;(2)设前n项和为 ,求
,求 的前
的前 项和为
项和为 .
. ;
; .
.