题目内容
已知D为△ABC的边BC上一点，且AB：BC：CA=1：
：1．
（1）求角A的大小；
（2）若△ABC的面积为
，且∠ADC=45°，求BD的长．
| 3 |
（1）求角A的大小；
（2）若△ABC的面积为
| 3 |
分析：设三边之比为k，表示出三边长，
（1）利用余弦定理表示出cosA，将三边长代入求出cosA的值，由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数；
（2）利用三角形的面积公式列出关系式，将已知面积与sinA的值代入求出AB的值，在三角形ABD中，利用正弦定理即可求出BD的长．
（1）利用余弦定理表示出cosA，将三边长代入求出cosA的值，由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数；
（2）利用三角形的面积公式列出关系式，将已知面积与sinA的值代入求出AB的值，在三角形ABD中，利用正弦定理即可求出BD的长．
解答：
解：设AB：BC：CA=1：
：1=k，则AB=AC=k，BC=
k，
（1）由余弦定理得：cosA=
=
=-
，
∵A为三角形的内角，∴A=120°；
（2）∵AB=CA，∠A=120°，
∴∠B=∠C=30°，
∴∠BAD=15°，
∵S△ABC=
AB•AC•sin120°=
，
∴AB=AC=2，
∵sin15°=sin（45°-30°）=sin45°cos30°-cos45°sin30°=
，
则由正弦定理
=
得：BD=
=
-1．
解：设AB：BC：CA=1：| 3 |
| 3 |
（1）由余弦定理得：cosA=
| AB2+CA2-BC2 |
| 2AB•CA |
k2+k2-(
| ||
| 2k2 |
| 1 |
| 2 |
∵A为三角形的内角，∴A=120°；
（2）∵AB=CA，∠A=120°，
∴∠B=∠C=30°，
∴∠BAD=15°，
∵S△ABC=
| 1 |
| 2 |
| 3 |
∴AB=AC=2，
∵sin15°=sin（45°-30°）=sin45°cos30°-cos45°sin30°=
| ||||
| 4 |
则由正弦定理
| AB |
| sin(180°-45°) |
| BD |
| sin15° |
| 2sin15 |
| sin135° |
| 3 |
点评：此题考查了正弦、余弦定理，三角形的面积公式，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
已知D为△ABC的边AC的中点，若
•
=
•
，则△ABC的形状必为（ ）
| BD |
| BC |
| BA |
| BD |
| A、等边三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
：1．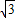
，且∠ADC=45°，求BD的长．