题目内容
1.在等比数列{an}中,a1+a2+a3+a4+a5=8,且$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+$\frac{1}{{a}_{4}}$+$\frac{1}{{a}_{5}}$=2,求a3.分析 由题意可得a3($\frac{1}{{q}^{2}}$+$\frac{1}{q}$+1+q+q2)=8,$\frac{1}{{a}_{3}}$(q2+q+1+$\frac{1}{q}$+$\frac{1}{{q}^{2}}$)=2,两式相除可得a3的方程,解方程可得.
解答 解:设等比数列{an}的公比为q,则等比数列{$\frac{1}{{a}_{n}}$}的公比为$\frac{1}{q}$,
由题意可得a1+a2+a3+a4+a5=a3($\frac{1}{{q}^{2}}$+$\frac{1}{q}$+1+q+q2)=8,①
$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+$\frac{1}{{a}_{4}}$+$\frac{1}{{a}_{5}}$=$\frac{1}{{a}_{3}}$(q2+q+1+$\frac{1}{q}$+$\frac{1}{{q}^{2}}$)=2,②
$\frac{①}{②}$可得${{a}_{3}}^{2}$=4,解得a3=2,或a3=-2
点评 本题考查等比数列数列的通项公式,属基础题.

练习册系列答案
相关题目
10.已知P是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1上的任意一点,F1,F2是它的左右焦点,且|PF1|=5,则|PF2|=( )
| A. | 1 | B. | 9 | C. | 1或9 | D. | 9或5 |
9.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F2的直线交双曲线的渐近线于A、B两点,若F1A⊥F2A,且$\overrightarrow{{F}_{2}B}$=3$\overrightarrow{A{F}_{2}}$,则双曲线的离心率为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
6.阅读如图的程序框图,运行相应的程序,则输出i的值( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.已知实数x、y满足$\left\{\begin{array}{l}y≥1\\ y≤2x-1\\ x+y≤m\end{array}\right.$,如果目标函数z=x-y的最小值为-1,则实数m等于( )
| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
10.已知等差数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=3,则$\frac{{S}_{12}}{{S}_{9}}$=( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
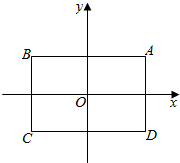 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的元二次一次方程$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上.则k•t的值等于1.
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的元二次一次方程$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上.则k•t的值等于1.