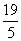题目内容
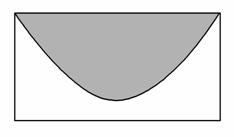
某广场中心建造一个花圃,花圃分成5个部分(如图).现有4种不同颜色的花可以栽种,若要求每部分必须栽种1种颜色的花且相邻部分不能栽种同样颜色的花,则不同的栽种方法有________种.
72
[解析] 依题意,按花圃的5个部分实际栽种花的颜色种数进行分类计数:第一类,花圃的5个部分实际栽种花的颜色种数是3时,满足题意的方法数共有A =24种;第二类,花圃的5个部分实际栽种花的颜色种数是4时,满足题意的方法数共有A
=24种;第二类,花圃的5个部分实际栽种花的颜色种数是4时,满足题意的方法数共有A ×2=48种.因此,满足题意的方法数共有24+48=72种.
×2=48种.因此,满足题意的方法数共有24+48=72种.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机调查了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入 (单位:百元) | [15, 25) | [25, 35) | [35, 45) | [45, 55) | [55, 65) | [65, 75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表,并回答是否有99%的把握认为“月收入以5500为分界点对‘楼市限购令’的态度有差异”;
|
| 月收入不低于55 百元的人数 | 月收入低于55 百元的人数 | 合计 |
| 赞成 | a= | c= | |
| 不赞成 | b= | d= | |
| 合计 |
(2)若对月收入在[15,25),[25,35)的被调查人中各随机选取1人进行追踪调查,求选中的2人中不赞成“楼市限购令”人数至多1人的概率.
| P(χ2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
K2=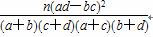
 B.
B.
 D.
D.
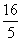 B.
B.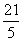
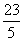 D.
D.