Question

【题目】函数，

（1）若，试讨论函数的单调性；

（2）若，试讨论的零点的个数；

Answer 1

【答案】（1）在和上为增函数，在上为减函数；（2）当时，函数有且仅有一个零点；

当或或或时，函数有两个零点；

当或时，有三个零点．

【解析】

试题把代入函数，根据绝对值不等式的几何意义去掉绝对值的符号，根据函数的解析式作出函数的图象，根据函数图象讨论函数的单调性；（2）把函数的零点转化为方程的根，作图和的图象，直线移动过程中注意在什么范围内有一个零点，在什么范围内有两个零点，三个零点，通过数形结合解决有关问题．

试题解析：（1）

图像如下：

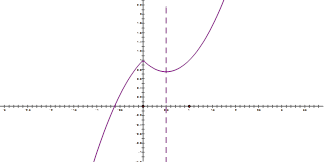
所以在和上为增函数，在上为减函数；

（2）的零点，除了零点以外的零点

即方程的根

作图和，如图可知：

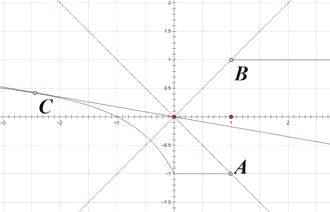
当直线的斜率：

当时有一根；

当时有两根；

当时，有一根；

当时，有一根；

当（当和相切时）没有实数根；

当（当和相切时）有一根；

当时有两根．

综上所述：

当时，函数有且仅有一个零点；

当或或或时，函数有两个零点；

当或时，有三个零点．