题目内容
已知圆O:x2+y2=4和点M(1,a).
(1)若过点M有且只有一条直线与圆O相切,求正数a的值,并求出切线方程;
(2)若a=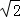 ,过点M的圆的两条弦AC,BD互相垂直.
,过点M的圆的两条弦AC,BD互相垂直.
①求四边形ABCD面积的最大值;②求|AC|+|BD|的最大值.
解:(1)由条件知点M在圆O上,所以1+a2=4,则a=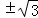 ,
,
由a>0,则a= ,点M为(1,
,点M为(1, ),kOM=
),kOM= ,切线的斜率为﹣
,切线的斜率为﹣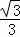 ,
,
此时切线方程为y﹣ =﹣
=﹣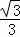 (x﹣1),即x+
(x﹣1),即x+ y﹣4=0;
y﹣4=0;
(2)设O到直线AC,BD的距离分别为d1,d2,
则d12+d22=|OM|2=3,于是|AC|=2 ,|BD|=2
,|BD|=2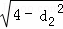 ,
,
①SABCD=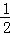 |AC|•|BD|=2
|AC|•|BD|=2 •
•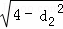 ≤4﹣d12+4﹣d22=8﹣3=5,
≤4﹣d12+4﹣d22=8﹣3=5,
当且仅当d1=d2=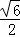 时取等号,
时取等号,
即四边形ABCD面积的最大值为5;
②|AC|+|BD|=2 +2
+2 ,
,
则(|AC|+|BD|)2=4(4﹣d12+4﹣d22+2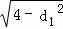 •
• )
)
=4(5+2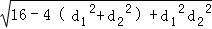 )=4(5+2
)=4(5+2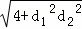 )
)
因为2d1d2≤d12+d22=3,所以d12d22≤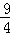 ,当且仅当d1=d2=
,当且仅当d1=d2=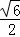 时取等号,
时取等号,
所以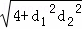 ≤
≤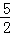 ,所以(|AC|+|BD|)2≤4(5+2×
,所以(|AC|+|BD|)2≤4(5+2×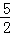 )=40,
)=40,
所以|AC|+|BD|≤2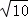 ,
,
即|AC|+|BD|的最大值为2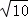 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
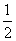
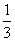 D.
D.
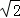 或
或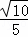 D. 2
D. 2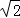
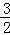 ,b=3 B. k=﹣
,b=3 B. k=﹣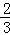 ,b=﹣3 C. k=﹣
,b=﹣3 C. k=﹣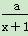 在区间[1,2]上都是减函数,则a的取值范围是( )
在区间[1,2]上都是减函数,则a的取值范围是( )