题目内容
设椭圆 的一个焦点为F,点P在y轴上,直线PF交椭圆于M、N,
的一个焦点为F,点P在y轴上,直线PF交椭圆于M、N, ,则实数λ1+λ2=
,则实数λ1+λ2=
- A.

- B.
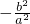
- C.

- D.

C
分析:设直线l的斜率为k,则直线l的方程是y=k(x-c).将直线l的方程代入到椭圆C的方程中,消去y并整理得(b2+a2k2)x2-2a2ck2x+a2c2k2-a2b2=0.然后利用向量关系及根与系数的关系,可求得λ1+λ2的值.
解答:设M,N,P点的坐标分别为M(x1,y1),N(x2,y2),P(0,y0),
又不妨设F点的坐标为(c,0).
显然直线l存在斜率,设直线l的斜率为k,
则直线l的方程是y=k(x-c).
将直线l的方程代入到椭圆C的方程中,消去y并整理得(b2+a2k2)x2-2a2ck2x+a2c2k2-a2b2=0.
∴ ,
, .
.
又∵ ,
,
将各点坐标代入得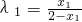 ,
,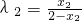
 =
= .
.
故选C.
点评:本题以向量为载体,考查直线与椭圆的位置关系,是椭圆性质的综合应用题,解题时要注意公式的合理选取和灵活运用.
分析:设直线l的斜率为k,则直线l的方程是y=k(x-c).将直线l的方程代入到椭圆C的方程中,消去y并整理得(b2+a2k2)x2-2a2ck2x+a2c2k2-a2b2=0.然后利用向量关系及根与系数的关系,可求得λ1+λ2的值.
解答:设M,N,P点的坐标分别为M(x1,y1),N(x2,y2),P(0,y0),
又不妨设F点的坐标为(c,0).
显然直线l存在斜率,设直线l的斜率为k,
则直线l的方程是y=k(x-c).
将直线l的方程代入到椭圆C的方程中,消去y并整理得(b2+a2k2)x2-2a2ck2x+a2c2k2-a2b2=0.
∴
 ,
, .
.又∵
 ,
,将各点坐标代入得
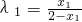 ,
,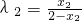
 =
= .
.故选C.
点评:本题以向量为载体,考查直线与椭圆的位置关系,是椭圆性质的综合应用题,解题时要注意公式的合理选取和灵活运用.

练习册系列答案
相关题目
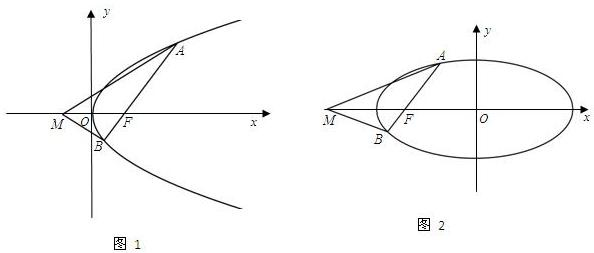
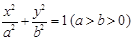 的一个焦点为F(2,0),离心率
的一个焦点为F(2,0),离心率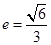 .
.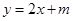 与椭圆交于不同的A,B两点,与y轴交于E点,且
与椭圆交于不同的A,B两点,与y轴交于E点,且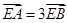 ,求实数m的值.
,求实数m的值. 的一个焦点为F,点P在y轴上,直线PF交椭圆于M、N,
的一个焦点为F,点P在y轴上,直线PF交椭圆于M、N, ,则实数λ1+λ2=( )
,则实数λ1+λ2=( )


