Question

（1）如图1所示，请证明抛物线的一个几何性质：过抛物线y²=4x的焦点F任作直线l与抛物线交于A，B两点，则在x轴上存在定点M（-1，0），使直线MF始终是∠AMB的平分线；
（2）如图2所示，对于椭圆

x2

5

+y2=1，设它的左焦点为F；请写出一个类似地性质；并证明其真假．

Answer 1

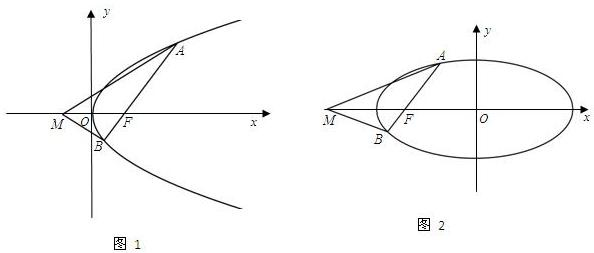
分析：（1）设直线l的方程为y=k（x-1），则由方程组

y=k(x-1) y2=4x

得关于x的一元二次方程，由根与系数的关系得x₁+x₂，x₁x₂，从而得直线MA，MB的斜率之和为0，即得直线MF平分∠AMB．
（2）同（1）类似，过椭圆

x2

5

+y2=1的左焦点F（-2，0）任作直线l与椭圆交于A，B两点，则在x轴上存在定点M，使直线MF始终平分∠AMB；证明与（1）相同，求出点M的坐标即可．

解答：解：（1）设直线l的方程为y=k（x-1）（k不存在时，显然成立）
则

y=k(x-1) y2=4x

得 k²x²-（2k²+4）x+k²=0∴x₁x₂=1，
∵kMA+kMB=

yA-0

xA+1

+

yB-0

xB+1

=

k(xA-1)

xA+1

+

k(xB-1)

xB+1

=

k(2xAxB-2)

(xA+1)(xB+1)

=0；
∴直线MF始终是∠AMB的平分线．
（2）过椭圆

x2

5

+y2=1的左焦点F（-2，0）任作直线l与椭圆交于A，B两点，则在x轴上存在定点M(-

5

2

，0)，使直线MF始终是∠AMB的平分线；
证明如下：设直线l的方程为y=k（x+2），（k不存在时，显然成立）；
由

y=k(x+2) x2 5 +y2=1

，得（1+5k²）x²+20k²x+20k²-5=0；∴

x1+x2= -20k2 1+5k2 x1x2= 20k2-5 1+5k2

，设M（t，0），则kMA+kMB=

yA-0

xA-t

+

yB-0

xB-t

=

k(xA+2)

xA-t

+

k(xB+2)

xB-t

=

k[2x1x2+(2-t)(x1+x2)-4t]

(x1-t)(x2-t)

；
将根与系数的关系式代入，得4t+10=0，即得点M(-

5

2

 ，0)．

点评：本题考查了直线与抛物线、椭圆的综合应用问题，也考查了类比推理的数学方法；解题时应灵活应用，细心解答．