Question

已知椭圆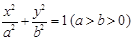的一个焦点为F（2，0），离心率.

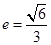(1)求椭圆的方程;

(2)设直线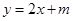与椭圆交于不同的A,B两点,与y轴交于E点,且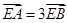,求实数m的值.

 

Answer 1

【答案】

（1）  （2）   

【解析】(1)由c和e,直接求出a,c的值.从而求出b的值.

（2）直线与椭圆联立消y后，得到关于x的一元二次方程，那么A、B两点的横坐标就是方程的两个根，再根据,可得x₁与x₂之间的关系，再借助韦达定理，就可以建立三个方程，消去x₂,x₁,解出m的值

解：

（1）由题意得       …………2分

所以椭圆的方程为……………4分

  （2）设,由         ………… 6分

得，且，∴ 

 …………①

在中，令x=0,得y=m,,即E（0，m）  …………………………8分

又，

…………②消去x₂,得，    ……10分

∴