题目内容
求下列凼数的单调区间：f（x）=x3+
．
| 3 |
| x |
考点：函数的单调性及单调区间
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：求出函数的定义域，求出函数的导数，令导数大于0，得增区间，令导数小于0，得减区间．
解答：
解：函数f（x）的定义域为{x|x≠0}．
f（x）=x3+
的导数为f′（x）=3x2-
=
=
，
当-1＜x＜0或0＜x＜1时，f′（x）＜0，f（x）递减，
当x＞1或x＜-1时，f′（x）＞0，f（x）递增．
则函数f（x）的单调增区间为（-∞，-1），（1，+∞），
单调减区间为（-1，0），（0，1）．
f（x）=x3+
| 3 |
| x |
| 3 |
| x2 |
| 3(x4-1) |
| x2 |
| 3(x-1)(x+1)(x2+1) |
| x2 |
当-1＜x＜0或0＜x＜1时，f′（x）＜0，f（x）递减，
当x＞1或x＜-1时，f′（x）＞0，f（x）递增．
则函数f（x）的单调增区间为（-∞，-1），（1，+∞），
单调减区间为（-1，0），（0，1）．
点评：本题考查函数的单调性，考查导数的运用，考查运算能力，属于基础题和易错题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
设函数f（x）=loga（x-a+2）在区间（1，+∞）上恒为正值，则实数a的取值范围是（ ）
| A、（1，2] | ||
| B、（1，2） | ||
| C、（0，1）∪（1，2） | ||
D、(1，
|
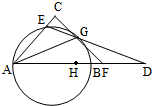过以AB为直径的圆上C点作直线交圆于E点，交AB延长线于D点，过C点作圆的切线交AD于F点，交AE延长线于G点，且GA=GF．