题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长轴为直径的圆与直线
的长轴为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知过点![]() 的动直线与椭圆
的动直线与椭圆![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的面积S的取值范围.
的面积S的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据直线与圆相切可得![]() ,再根据离心率得
,再根据离心率得![]() ,(2)设动直线方程,并联立直线和椭圆方程,利用韦达定理与弦长公式得
,(2)设动直线方程,并联立直线和椭圆方程,利用韦达定理与弦长公式得![]() ,根据点到直线距离公式得三角形的高,代入三角形面积公式得
,根据点到直线距离公式得三角形的高,代入三角形面积公式得![]() ,最后结合基本不等式求取值范围.
,最后结合基本不等式求取值范围.
(1)由离心率为![]() ,
,
因为椭圆C的长轴为直径的圆与直线![]() 相切,
相切,
所以![]() ,
,
即椭圆![]() 的标准方程
的标准方程![]() .
.
(2)设动直线方程为![]() ,点
,点![]() ,且
,且![]() ,
,
联立直线和椭圆方程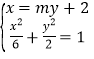 ,
,
消元得![]() ,
,
则![]() ,
,
因为原点![]() 到直线
到直线![]() 距离为
距离为![]() ,
,
则![]() 的面积
的面积![]() ,
,
令![]() ,则
,则![]() ,
,
又![]() (当且仅当
(当且仅当![]() 时取等号),则
时取等号),则![]() ,
,
即![]() 的面积S的取值范围为
的面积S的取值范围为![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】下面四个命题,
(1)函数![]() 在第一象限是增函数;
在第一象限是增函数;
(2)在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充分非必要条件;
”的充分非必要条件;
(3)函数![]() 图像关于点
图像关于点![]() 对称的充要条件是
对称的充要条件是![]() ;
;
(4)若![]() ,则
,则![]() .
.
其中真命题的是_________.(填所有真命题的序号)
【题目】某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分两层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2:
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 | x | 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 | y | 36 | 18 |
(1)求x,y的值;
(2)在答题纸上完成频率分布直方图;并根据频率分布直方图,估计该工厂B类工人生产能力的平均数(同一组中的数据用该区间的中点值作代表)和中位数.(结果均保留一位小数)



