题目内容
设函数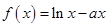 .
.
(1)当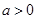 时,求函数
时,求函数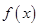 在区间
在区间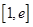 内的最大值;
内的最大值;
(2)当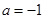 时,方程
时,方程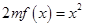 有唯一实数解,求正数
有唯一实数解,求正数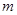 的值.
的值.
(1)详见解析;(2)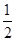 .
.
解析试题分析:(1)先求出导数方程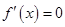 的根,对此根与区间
的根,对此根与区间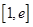 的位置关系进行分类讨论,确定函数在区间
的位置关系进行分类讨论,确定函数在区间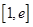 上的单调性,从而求出函数
上的单调性,从而求出函数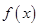 在区间
在区间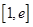 上的最大值;(2)构造函数
上的最大值;(2)构造函数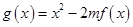 ,
,
利用导数求出函数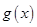 的极值点
的极值点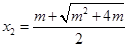 ,并确定函数
,并确定函数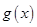 的单调性,得到
的单调性,得到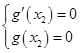 ,消去
,消去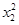 并化简得到
并化简得到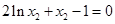 ,通过构造函数
,通过构造函数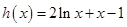 并利用导数研究函数
并利用导数研究函数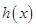 的单调性并结合
的单调性并结合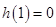 ,得到
,得到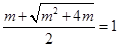 ,从而求出
,从而求出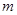 的值.
的值.
(1)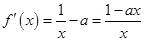 ,
,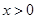 ,
,
令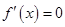 得
得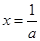 . 因为
. 因为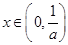 时,
时,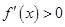 ,
,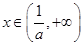 时,
时,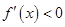 ,
,
所以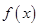 在
在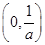 递增,在
递增,在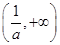 递减;
递减;
①当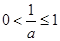 时,即
时,即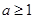 时,
时,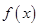 在
在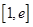 上递减,
上递减,
所以 时
时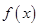 取最大值
取最大值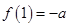 ;
;
②当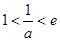 时,即
时,即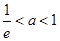 时,
时,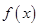 在
在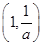 递增,在
递增,在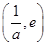 递减,
递减,
所以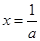 时,
时,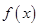 取最大值
取最大值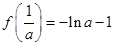 ;
;
③当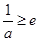 即
即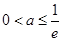 时,
时,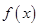 在
在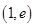 递增,
递增,
所以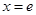 时
时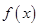 取最大值
取最大值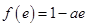 ;
;
(2)因为方程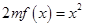 有唯一实数解,即
有唯一实数解,即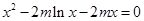 有唯一实数解,
有唯一实数解,
设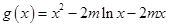 ,则
,则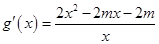 ,
,
令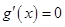 ,
,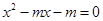 ,因为
,因为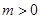 ,
,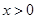 ,
,
所以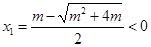 (舍去),
(舍去),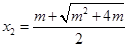 ,
,
当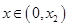 时,
时,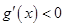 ,
,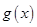 在
在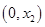 上单调递减,
上单调递减,
当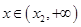 时,
时,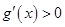 ,
,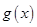 在
在 上单调递增,
上单调递增,
所以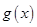 最小值为
最小值为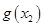 ,
,
则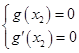

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 在
在 处取得极值-2.
处取得极值-2. 的解析式;
的解析式;  在点
在点 处的切线方程.
处的切线方程.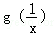 的大小关系;
的大小关系; 对任意x>0成立.
对任意x>0成立.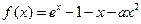 。
。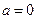 ,求
,求 的单调区间;
的单调区间;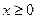 时,
时,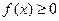 ,求a的取值范围。
,求a的取值范围。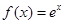 ,
,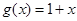 .
.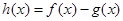 的最小值;
的最小值;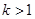 ,证明:当
,证明:当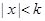 时,
时,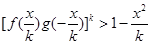 .
. .
. 在点
在点 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值; 时,求
时,求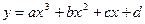 满足下列条件:
满足下列条件: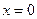 处导数为-1;③在
处导数为-1;③在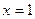 处切线方程为
处切线方程为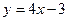 .
.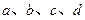 的值;
的值;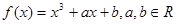 的图象记为E.过点
的图象记为E.过点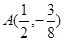 作曲线E的切线,这样的切线有且仅有两条,求
作曲线E的切线,这样的切线有且仅有两条,求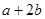 的值.
的值.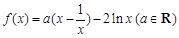 .
.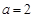 ,求曲线
,求曲线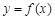 在点
在点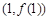 处的切线方程;
处的切线方程;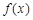 的单调区间;
的单调区间;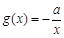 .若至少存在一个
.若至少存在一个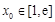 ,使得
,使得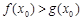 成立,求实数
成立,求实数 的取值范围.
的取值范围.