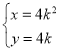题目内容
【题目】已知抛物线
的准线过椭圆C：
（a＞b＞0）的左焦点F，且点F到直线l：
（c为椭圆焦距的一半）的距离为4.
（1）求椭圆C的标准方程；
（2）过点F做直线与椭圆C交于A，B两点，P是AB的中点，线段AB的中垂线交直线l于点Q.若
，求直线AB的方程.
【答案】（1）
；（2）
或
.
【解析】
（1）由抛物线的准线方程求出
的值，确定左焦点
坐标，再由点F到直线l：
的距离为4，求出
即可；
（2）设直线方程，与椭圆方程联立，运用根与系数关系和弦长公式，以及两直线垂直的条件和中点坐标公式，即可得到所求直线的方程.
（1）抛物线
的准线方程为
，
，直线
，点F到直线l的距离为
，
，
所以椭圆
的标准方程为；
（2）依题意
斜率不为0，又过点，设方程为
，
联立
，消去
得，
，
，设
，
，
，
，
线段AB的中垂线交直线l于点Q，所以
横坐标为3，
，
，
，平方整理得
，
解得
或
（舍去），
，
所求的直线方程为或.
练习册系列答案
相关题目
