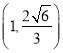题目内容
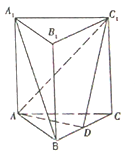
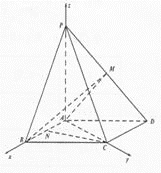
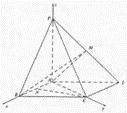
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() 是棱PD的中点,且
是棱PD的中点,且![]() ,
, ![]() .
.
(I)求证: ![]() ; (Ⅱ)求二面角
; (Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 是
是![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 成角的正弦值为
成角的正弦值为![]() ,求
,求![]() 的值.
的值.

【答案】(I)见解析;(Ⅱ) ![]() ;(Ⅲ)1.
;(Ⅲ)1.
【解析】试题分析:(1)![]() ,
,![]() ,所以
,所以![]() 平面PAC;(2)建立空间直角坐标系,求出两个法向量,平面MAB的法向量
平面PAC;(2)建立空间直角坐标系,求出两个法向量,平面MAB的法向量![]() ,
,![]() 是平面ABC的一个法向量,求出二面角;(3)设
是平面ABC的一个法向量,求出二面角;(3)设![]() ,平面MAB的法向量
,平面MAB的法向量![]() ,解得答案。
,解得答案。
试题解析:
证明:(I)连结AC.因为为在![]() 中,
中,
![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
因为AB//CD,所以![]() .
.
又因为![]() 地面ABCD,所以
地面ABCD,所以![]() .因为
.因为![]() ,
,
 所以
所以![]() 平面PAC.
平面PAC.
(II)如图建立空间直角坐标系,则![]() .
.
因为M是棱PD的中点,所以![]() .
.
所以![]() ,
,![]() .
. ![]() 为平面MAB的法向量,
为平面MAB的法向量,
所以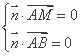 ,即
,即![]() ,令
,令![]() ,则
,则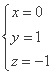 ,
,
所以平面MAB的法向量![]() .因为
.因为![]() 平面ABCD,
平面ABCD,
所以![]() 是平面ABC的一个法向量.
是平面ABC的一个法向量.
所以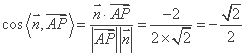 .因为二面角
.因为二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的大小为
的大小为![]() .
.
(III)因为N是棱AB上一点,所以设![]() ,
,![]() .
.
 设直线CN与平面MAB所成角为
设直线CN与平面MAB所成角为![]() ,
,
因为平面MAB的法向量![]() ,
,
所以 .
.
解得![]() ,即
,即![]() ,
,![]() ,所以
,所以![]() .
.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。

区间 |
|
|
|
|
|
人数 |
| a | b |
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。