题目内容
【题目】已知⊙H被直线x-y-1=0,x+y-3=0分成面积相等的四个部分,且截x轴所得线段的长为2。
(I)求⊙H的方程;
(Ⅱ)若存在过点P(0,b)的直线与⊙H相交于M,N两点,且点M恰好是线段PN的中点,求实数b的取值范围
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(I)设![]() 的方程为
的方程为![]() ,由题意可知圆心
,由题意可知圆心![]() 一定是两直线
一定是两直线![]() 的交点,可得交点为
的交点,可得交点为![]() ,所以
,所以![]() . 又
. 又![]() 截x轴所得线段的长为2,所以
截x轴所得线段的长为2,所以![]() .,即可得到⊙H的方程;
.,即可得到⊙H的方程;
(II)法一:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,
,
过点N作![]() 的直径
的直径![]() ,连结
,连结![]() .
.
由题可得“点![]() 是线段
是线段![]() 的中点”等价于“圆上存在一点
的中点”等价于“圆上存在一点![]() 使得
使得![]() 的长等于
的长等于![]() 的直径”.
的直径”.
由此得到实数b的取值范围
法二:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,连结
,连结![]() ,
,
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,并设
,并设![]() .
.
由题意得![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,由此得到实数b的取值范围
,由此得到实数b的取值范围
试题解析:(I)设![]() 的方程为
的方程为![]() ,
,
因为![]() 被直线
被直线![]() 分成面积相等的四部分,
分成面积相等的四部分,
所以圆心![]() 一定是两直线
一定是两直线![]() 的交点,
的交点,
易得交点为![]() ,所以
,所以![]() .
.
又![]() 截x轴所得线段的长为2,所以
截x轴所得线段的长为2,所以![]() .
.
所以![]() 的方程为
的方程为![]() .
.
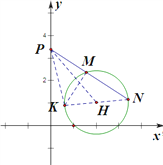
(II)法一:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,
,
过点N作![]() 的直径
的直径![]() ,连结
,连结![]() .
.
当![]() 与
与![]() 不重合时,
不重合时, ![]() ,
,
又点![]() 是线段
是线段![]() 的中点
的中点![]() ;
;
当![]() 与
与![]() 重合时,上述结论仍成立.
重合时,上述结论仍成立.
因此,“点![]() 是线段
是线段![]() 的中点”等价于“圆上存在一点
的中点”等价于“圆上存在一点![]() 使得
使得![]() 的长等于
的长等于![]() 的直径”.
的直径”.
由图可知![]() ,即
,即![]() ,即
,即![]() .
.
显然![]() ,所以只需
,所以只需![]() ,即
,即![]() ,解得
,解得![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.

法二:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,连结
,连结![]() ,
,
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,并设
,并设![]() .
.
由题意得![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
将![]() 代入整理可得
代入整理可得![]() ,
,
因为![]() ,所以
,所以![]() ,,解得
,,解得![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目