题目内容
8.已知函数f(x)=$\frac{{x}^{2}+5x+5}{{e}^{x}}$.(1)求f(x)的极大值;
(2)求f(x)在区间(-∞,0]上的最小值;
(3)若x2+5x+5-aex≥0,求a的取值范围.
分析 (1)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极大值即可;
(2)根据函数的单调性,求出函数在闭区间的最小值即可;
(3)问题转化为$a≤\frac{{{x^2}+5x+5}}{e^x}=f(x)$,根据函数的单调性得到函数f(x)在区间(-∞,0]上有最小值-e3,从而求出a的范围即可.
解答 解:(1)${f^'}(x)=\frac{-x(x+3)}{e^x}$…(1分)
当x<-3时,f′(x)<0
当-3<x<0时,f′(x)>0
当x>0时,f′(x)<0…(3分)
所以函数f(x)在(-∞,-3)上为单调递减函数
在(-3,0)上为单调递增函数
在(0,+∞)上为单调递减函数…(4分)
因此函数f(x)在x=0处有极大值f(0)=5 …(5分)
(2)由(1)得函数f(x)在(-∞,-3)上为单调递减函数,
在(-3,0)上为单调递增函数
所以函数f(x)在x=-3处有最小值f(-3)=-e3…(7分)
(3)$a≤\frac{{{x^2}+5x+5}}{e^x}=f(x)$…(9分)
由(2)得函数f(x)在区间(-∞,0]上有最小值-e3…(10分)
当x>0时,f(x)>0 …(11分)
所以函数f(x)在定义域中的最小值为-e3,所以a≤-e3
即a的取值范围为(-∞,-e3]…(12分)
点评 本题考查了函数的单调性、最值、极值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
3.将二次函数y=x2的图象向下平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
17.函数$y=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,则( )
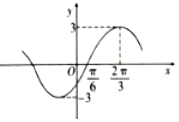

| A. | $y=3sin({2x-\frac{π}{6}})$ | B. | $y=3sin({2x-\frac{π}{3}})$ | C. | $y=3sin({x-\frac{π}{6}})$ | D. | $y=3sin({x-\frac{π}{3}})$ |