题目内容
若Rt△ABC所在平面外一点P到△ABC的三个顶点距离相等.求证:过点P和△ABC斜边中点的直线必垂直于三角形所在的平面.
思路分析:如图2-3-7,Rt△ABC中,∠C=90°,D为斜边AB中点.

图2-3-7
在△PDA与△PDB中,PA=PB,PD=PD,AD=BD,这两个三角形全等.
所以∠PDA=∠PDB=90°,同时可有△PDA和△PDC全等,
所以∠PDC=∠PDA=90°,问题得证.
证明:∵PA=PB,PD=PD,AD=BD,
∴△PDA≌△PDB.
∴∠PDA=∠PDB.
又∠PDA+∠PDB=180°,
∴∠PDA=∠PDB=90°.
∴PD⊥AB.
同理△PDA≌△PDC.
∴∠PDC=∠PDA=90°.
∴PD⊥DC.
又DC与AB相交,
∴PD⊥平面ABC.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
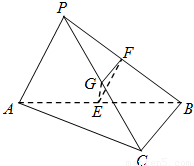
 如图,点P是Rt△ABC所在平面外一点,∠ABC=90°,点P在平面ABC上的射影在AB上,E、F、G分别为AB、PB、PC的中点.若PA=BC=4,求△EFG的面积.
如图,点P是Rt△ABC所在平面外一点,∠ABC=90°,点P在平面ABC上的射影在AB上,E、F、G分别为AB、PB、PC的中点.若PA=BC=4,求△EFG的面积.