题目内容
如图,点P是Rt△ABC所在平面外一点,∠ABC=90°,点P在平面ABC上的射影在AB上,E、F、G分别为AB、PB、PC的中点.若PA=BC=4,求△EFG的面积.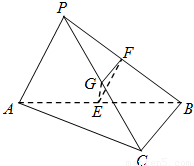
【答案】分析:先由三垂线定理证明PA⊥BC,再根据三角形的中位线平行第三边且等于第三边的一半,证明EF平行PA,且等于PA的一半,
GF平行与BC且等于BC的一半,就可判断△EFG为直角三角形且两条直角边长度已知,再利用直角三角形的面积公式求出面积即可.
解答: 解:∵点P在平面ABC上的射影在AB上,
解:∵点P在平面ABC上的射影在AB上,
∴PA在平面ABC上的射影在AB上.
又∠ABC=90°,∴AB⊥BC,
由三垂线定理得PA⊥BC.
∵E、F、G分别为AB、PB、PC的中点,且PA=BC=4,
∴EF∥PA,EF= PA,,GF∥BC,GF=
PA,,GF∥BC,GF= BC,
BC,
∴EF=GF=2,EF⊥GF,
∴ .
.
点评:本题主要考查立体几何中面面垂直,线线平行的判定,以及三角形面积的求法.
GF平行与BC且等于BC的一半,就可判断△EFG为直角三角形且两条直角边长度已知,再利用直角三角形的面积公式求出面积即可.
解答:
 解:∵点P在平面ABC上的射影在AB上,
解:∵点P在平面ABC上的射影在AB上,∴PA在平面ABC上的射影在AB上.
又∠ABC=90°,∴AB⊥BC,
由三垂线定理得PA⊥BC.
∵E、F、G分别为AB、PB、PC的中点,且PA=BC=4,
∴EF∥PA,EF=
 PA,,GF∥BC,GF=
PA,,GF∥BC,GF= BC,
BC,∴EF=GF=2,EF⊥GF,
∴
 .
.点评:本题主要考查立体几何中面面垂直,线线平行的判定,以及三角形面积的求法.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
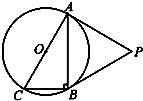 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB. 如图,P是Rt△ABC的斜边BC上异于B、C的一点,若过点P作直线l截△ABC,使截得的三角形与△ABC相似,则直线l共有( )
如图,P是Rt△ABC的斜边BC上异于B、C的一点,若过点P作直线l截△ABC,使截得的三角形与△ABC相似,则直线l共有( )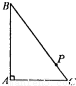
 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.
 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.