题目内容
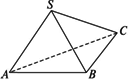
已知Rt△ABC所在平面外一点S满足SA=SB=SC,D为斜边AC的中点.(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
证明:(1)如图,取AB的中点M,连结SM、DM.
因SA=SB,
∴SM⊥AB.
又DM∥BC,
而AB⊥BC,
∴DM⊥AB.∴AB⊥面SDM.
而DS
面SDM,
∴SD⊥AB.又SA=SC,∴SD⊥AC.
故SD⊥面ABC.
(2)若AB=BC,∴BD⊥AC.
又由(1)知SD⊥BD,SD∩AC=D,
∴BD⊥面SAC.
练习册系列答案
应用题作业本系列答案
相关题目
cm．求点P到平面ABC的距离．
），顶点C在
轴上。
与Rt△ABC外接圆相切于第一象限，求切线与两坐标轴所围成的三角形面积最小时的切线方程。