题目内容
12.设α,β,γ为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:①若α⊥γ,β⊥γ,则α∥β;
②若α∥β,l?α,则l∥β;
③若m?α,n?α,m∥β,n∥β,则α∥β;
④若l⊥α,l∥β,则α⊥β
其中命题正确的是②④.(填序号)
分析 ①若α⊥γ,β⊥γ,则α∥β,研究与 同一平面垂直的两个平面之间的关系,面面平行的条件判断;
②若α∥β,l?α,则,利用平面与平面平行的性质,可得l∥β;
③若m?α,n?α,m∥β,n∥β,m,n不一定相交,则α∥β不正确;
④由面面垂直的判定定理可由l∥β得出α⊥β.
解答 解:①若α⊥γ,β⊥γ,则α∥β,此命题不正确,因为垂直于同一平面的两个平面可能平行、相交,不能确定两平面之间是平行关系,故不正确;
②若α∥β,l?α,则,利用平面与平面平行的性质,可得l∥β,正确;
③若m?α,n?α,m∥β,n∥β,m,n不一定相交,则α∥β不正确;
④由题意l⊥α,当l∥β时,必存在β内的直线l′,使l∥l′,可得l′⊥α,由面面垂直的判定定理可得α⊥β,正确.
故答案为:②④.
点评 本题考查平面的基本性质及推论,解题的关键是有着较强的空间感知能力及对空间中线面,面面,线线位置关系的理解与掌握,此类题是训练空间想像能力的题,属于基本能力训练题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
2. 设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
 设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {x|0<x≤1} | D. | {x|x≤1} |
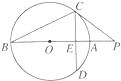 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.