题目内容
20．
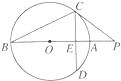如图，PC切圆O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，若圆O的半径为2，PA=1，求PC•CE的值．
分析 连接OC，得RT△OPC，求出PC即可，由射影定理得：PC2=PE•PO，从而求出PE，进而求出OE的长．
解答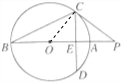 
解：PC切圆O于点C，连接OC，
∴OC⊥PC，
∵OC=2，OP=PA+AO=3，
在RT△OPC中，PC=$\sqrt{5}$，
又∵弦CD⊥AB于点E，
∴PC2=PE•PO，即5=PE•3，
∴PE=$\frac{5}{3}$，
∴PC•CE=$\frac{5\sqrt{5}}{3}$．
点评 本题考查了勾股定理，射影定理，圆的切线的性质，是一道基础题．
练习册系列答案
小学期末标准试卷系列答案
相关题目
11．
如图所示的是一个几何体的三视图，已知侧视图是一个等边三角形，根据图中尺寸可知这个几何体的表面积是（ ）
如图所示的是一个几何体的三视图，已知侧视图是一个等边三角形，根据图中尺寸可知这个几何体的表面积是（ ）| A． | 18+$\sqrt{3}$ | B． | $\frac{21\sqrt{3}}{2}$ | C． | 18+2$\sqrt{3}$ | D． | 6+2$\sqrt{3}$ |