题目内容
在△ABC中,E,F分别为边AB,AC上的点,且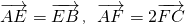 ,若
,若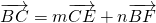 ,则m+n=________.
,则m+n=________.
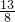
分析:在三角形ABC中,利用向量减法的三角形法则得
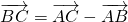 ,同样在三角形ABF中有
,同样在三角形ABF中有 ,在三角形AEC中有
,在三角形AEC中有 ,再结合条件
,再结合条件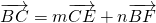 得
得 =(
=( m+n)
m+n) +(
+( n-m)
n-m) ,再利用向量相等的概念,得到关于m,n的方程.即可求解.
,再利用向量相等的概念,得到关于m,n的方程.即可求解.解答:
 解:在三角形ABC中,
解:在三角形ABC中,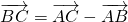 ,
,在三角形ABF中,∵
 ,
,∴
 ,?
,? ,
,在三角形AEC中,∵
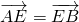 ,
,∴
 =
= ,?
,?
∵
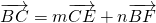 ,
,∴
 =m(
=m( )+n(
)+n( ),
),即
 =(
=( m+n)
m+n) +(
+( n-m)
n-m) ,
,∵
 不共线,
不共线,∴
 ,解得
,解得
则m+n=-
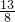 ,
,故答案为:
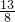
点评:本题考查了平面向量的基本定理及其意义,以及共线定理,同时考查了计算能力,属于基础题.

练习册系列答案
相关题目
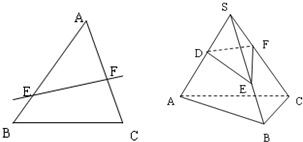 在△ABC中,E、F分别为AB、AC上的点,若
在△ABC中,E、F分别为AB、AC上的点,若