题目内容
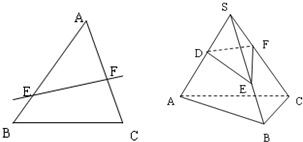在△ABC中，E、F分别为AB、AC上的点，若| AE |
| AB |
| AF |
| AC |
| S△AEF |
| S△ABC |
| SD |
| DA |
| SE |
| EB |
| SF |
| FC |
| VS-DEF |
| VS-ABC |
分析：在由平面图形的性质向空间物体的性质进行类比时，常用的思路有：由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质．由在△ABC中，E、F分别为AB、AC上的点，若
=m，
=n，则
=mn（面的性质），我们可以推断：在三棱锥S-ABC中，D、E、F分别是侧棱SA、SB、SC上的点，若
=m，
=n，
=p时，三棱锥的体积的性质．
| AE |
| AB |
| AF |
| AC |
| S△AEF |
| S△ABC |
| SD |
| DA |
| SE |
| EB |
| SF |
| FC |
解答：解：在类比推理时，我们可以
由平面图形中点的性质类比推理出空间里的线的性质，
由平面图形中线的性质类比推理出空间中面的性质，
由平面图形中面的性质类比推理出空间中体的性质．
由在△ABC中，E、F分别为AB、AC上的点，
若
=m，
=n，则
=mn（面的性质），
我们可以推断：在三棱锥S-ABC中，D、E、F分别是侧棱SA、SB、SC上的点，
若
=m，
=n，
=p时，
=
．
故答案为：
．
由平面图形中点的性质类比推理出空间里的线的性质，
由平面图形中线的性质类比推理出空间中面的性质，
由平面图形中面的性质类比推理出空间中体的性质．
由在△ABC中，E、F分别为AB、AC上的点，
若
| AE |
| AB |
| AF |
| AC |
| S△AEF |
| S△ABC |
我们可以推断：在三棱锥S-ABC中，D、E、F分别是侧棱SA、SB、SC上的点，
若
| SD |
| DA |
| SE |
| EB |
| SF |
| FC |
| VS-DEF |
| VS-ABC |
| mnp |
| (m+1)(n+1)(p+1) |
故答案为：
| mnp |
| (m+1)(n+1)(p+1) |
点评：本题考查的知识点是类比推理，在由平面图形的性质向空间物体的性质进行类比时，常用的思路有：由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质．
练习册系列答案
阅读快车系列答案
相关题目