题目内容
在△ABC中，E，F分别为AB，AC的中点，P为EF上的任一点，实数x，y满足
+
+y
=
，设△ABC，△PBC，△PCA，△PAB的面积分别为S，S1，S2，S3，记
=λ1，
=λ2，
=λ3，则λ2•λ3取到最大值时，2x+y的值为（ ）
| PA |
| xPB |
| PC |
| 0 |
| S1 |
| S |
| S2 |
| S |
| S3 |
| S |
分析：根据三角形中位线的性质，可得P到BC的距离等于△ABC的BC边上高的一半，从而得到S1=
S=S2+S3．由此结合基本不等式求最值，得到当λ2•λ3取最大值时点P在EF的中点．再由向量的加法的四边形法则，算出2
+
+
=
，结合已知条件的等式，可求出x、y的值，从而算出2x+y的值．
| 1 |
| 2 |
| PA |
| PB |
| PC |
| 0 |
解答：解：由题意，可得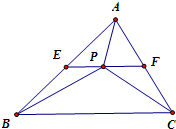
∵EF是△ABC的中位线，
∴P到BC的距离等于△ABC的BC边上高的一半，可得S1=
S=S2+S3
由此可得λ2•λ3=
≤
=
当且仅当S2=S3时，即P为EF的中点时，等号成立．
∴
+
=
由向量的加法的四边形法则可得，
+
=2
，
+
=2
∴两式相加，得2
+
+
=
∵由已知得
+
+y
=
∴根据平面向量基本定理，得x=y=
，从而得到2x+y=
综上所述，可得当λ2•λ3取到最大值时，2x+y的值为
故选：D
∵EF是△ABC的中位线，
∴P到BC的距离等于△ABC的BC边上高的一半，可得S1=
| 1 |
| 2 |
由此可得λ2•λ3=
| S2S3 |
| S2 |
(
| ||
| S2 |
| 1 |
| 16 |
当且仅当S2=S3时，即P为EF的中点时，等号成立．
∴
| PE |
| PF |
| 0 |
由向量的加法的四边形法则可得，
| PA |
| PB |
| PE |
| PA |
| PC |
| PF |
∴两式相加，得2
| PA |
| PB |
| PC |
| 0 |
∵由已知得
| PA |
| xPB |
| PC |
| 0 |
∴根据平面向量基本定理，得x=y=
| 1 |
| 2 |
| 3 |
| 2 |
综上所述，可得当λ2•λ3取到最大值时，2x+y的值为
| 3 |
| 2 |
故选：D
点评：本题给出三角形中的向量等式，在已知面积比λ2、λ3的积达到最大值的情况下求参数x、y的值，着重考查了运用基本不等式求最值、平面向量的加法法则和平面向量基本定理等知识，属于中档题．
练习册系列答案
相关题目
在△ABC中，E、F分别为AB、AC上的点，若