Question

（ （14分）已知双曲线的中心在原点，焦点F₁、F₂在坐标轴上，离心率为且过点(4，-)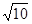

（Ⅰ）求双曲线方程；

（Ⅱ）若点M(3,m)在双曲线上，求证：点M在以F₁F₂为直径的圆上；

（Ⅲ）求△F₁MF₂的面积.

 

Answer 1

【答案】

 

(1) x²-y²=6

(2) 略

(3) 6

【解析】解：（Ⅰ） ∵离心率e=

∴设所求双曲线方程为x²-y²=(≠0)

则由点(4，-)在双曲线上

知=4²-(-)²=6

∴双曲线方程为x²-y²=6                                       

       （Ⅱ）若点M(3,m)在双曲线上

   则3²-m²=6     ∴m²=3

   由双曲线x²-y²=6知F₁(2,0),F₂(-2,0)

   ∴

   ∴,故点M在以F₁F₂为直径的双曲线上.             

（Ⅲ）=×2C×|M|=C|M|=2×=6