题目内容
7.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,经过点($\sqrt{3}$,$\frac{1}{2}$)(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点M(-1,0)作直线交椭圆于A,B两点,O是坐标原点,求△OAB的面积的最大值,并求此时直线l的方程.
分析 (Ⅰ)由题意,利用离心率公式及待定系数法即可求得a和b的值,求得椭圆的方程;
(Ⅱ)设直线l方程,代入椭圆方程,利用韦达定理及弦长公式和三角形的面积公式,利用换元法即可求得△OAB的面积的最大值及直线l的方程.
解答 解:(Ⅰ)由题意得e=$\frac{c}{a}$=$\frac{{\sqrt{3}}}{2}$,则a2=$\frac{4}{3}$c2,则a2=$\frac{1}{4}$b2,
将点($\sqrt{3}$,$\frac{1}{2}$)代入椭圆方程$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得:b2=1,a2=4,
∴所求的椭圆方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)设直线l方程l:x=hy-1
联立,$\left\{\begin{array}{l}{x^2}+4{y^2}=4\\ x=hy-1\end{array}\right.$
得:(4+h2)y2-2hy-3=0
因为△=16(h2+3)>0
所以${y_1}+{y_2}=\frac{2h}{{4+{h^2}}}$…(8分)
所以$S=\frac{1}{2}•|{OM}|•|{{y_1}-{y_2}}|=\frac{1}{2}•\frac{{\sqrt{△}}}{{4+{h^2}}}=\frac{{2\sqrt{{h^2}+3}}}{{{h^2}+4}}$
令$\sqrt{{h^2}+3}=t≥\sqrt{3}$
则$S=\frac{2t}{{{t^2}+1}}=\frac{2}{{t+\frac{1}{t}}}$在$[\sqrt{3},+∞)$上单调递减,
当$t=\sqrt{3}$即h=0时,${S_{max}}=\frac{{\sqrt{3}}}{2}$此时l:x=-1,
点评 本题考查椭圆标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理及弦长公式,函数的单调性的应用,属于中档题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 若a⊥α,b?α,则a⊥b | B. | 若a⊥α,a∥b,则b⊥α | ||
| C. | 若a⊥b,b⊥α,则a∥α或a?α | D. | 若a∥α,b?α,则a∥b |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
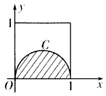 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )| A. | 157 | B. | 314 | C. | 486 | D. | 628 |
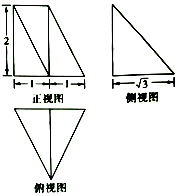 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$$\sqrt{3}$ | D. | $\frac{5}{3}$$\sqrt{3}$ |
| A. | $y=±\sqrt{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | $y=±\frac{1}{3}x$ | D. | y=±3x |