题目内容
若正实数a，b，c满足：3a-2b+c=0，则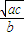
的最大值为 ．
【答案】分析：根据题意，由3a-2b+c=0可得3a+c=2b，将其代入
，消去b可得t=
，结合基本不等式的性质可得3
+
的最小值，由分式的性质可得
的最大值，即可得答案．
解答：解：根据题意，设t=
，
由3a-2b+c=0可得3a+c=2b，
则t=
=
=
=
；
又由3
+
≥2
，
则t≤
=
，即
的最大值为
；
故答案为
．
点评：本题考查基本不等式的运用，关键将3a-2b+c=0变形为3a+c=2b，进而运用换元法对
分析．
，消去b可得t=，结合基本不等式的性质可得3+的最小值，由分式的性质可得的最大值，即可得答案．解答：解：根据题意，设t=
，由3a-2b+c=0可得3a+c=2b，
则t=
===；又由3
+≥2，则t≤
=，即的最大值为；故答案为
．点评：本题考查基本不等式的运用，关键将3a-2b+c=0变形为3a+c=2b，进而运用换元法对
分析． 
练习册系列答案
相关题目
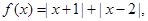不等式
在
上恒成立.
求
的最大值.