题目内容
（3）（本小题满分7分）选修4—5：不等式选讲
已知函数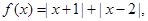
不等式
在
上恒成立.
（Ⅰ）求实数t的取值范围；
（Ⅱ）记t的最大值为T，若正实数a、b、c满足
求
的最大值.
【答案】
（Ⅰ）
．
（Ⅱ）
的最大值为
，当且仅当
，
，
时等号成立．
【解析】(I)因为
，所以可得f(x)的最小值为3,所以
在
上恒成立,即可得到
.
(II) 由（Ⅰ）知，
，即
．
由柯西不等式知：
，则
．
所以的最大值为，要注意求等的条件为a=2b=c= 
.
（Ⅰ）不等式在
上恒成立，则
，
又因为，所以函数
的最小值为
，
所以
的取值范围为． ……3分
（Ⅱ）由（Ⅰ）知，，即．
由柯西不等式知：
，则．
所以的最大值为， ……6分
当且仅当，，时等号成立． ……7分
练习册系列答案
相关题目
，N=
，且MN=
。
=2
sin
。
3的解集为
，求实数a的值；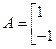
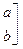,A的一个特征值
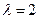，其对应的特征向量是
.
；
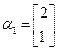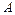在矩阵M所对应的线性变换下的像的方程
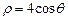．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：
，
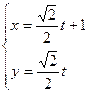求直线l与曲线C相交所成的弦的弦长．
,A的一个特征值
，其对应的特征向量是
.
；
在矩阵M所对应的线性变换下的像的方程
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：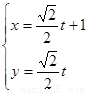
，求直线l与曲线C相交所成的弦的弦长．
及对应的一个特征向量
，并且矩阵M对应的变换将点
变换成
，求矩阵M。
的直线
与圆C：
（
为参数）相交于A、B两点，试确定
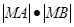的值。
满足
，
，试确定
的最大值。