题目内容
15．如果A={x|x＞-1}，那么（ ）| A． | 0?A | B． | {0}∈A | C． | ∅∈A | D． | {0}⊆A |
分析 利用元素与集合的关系，集合与集合关系判断选项即可．
解答 解：A={x|x＞-1}，由元素与集合的关系，集合与集合关系可知：{0}⊆A．
故选：D．
点评 本题考查元素与集合的关系，集合基本知识的应用，是基础题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
5．设α-l-β是二面角，直线a在平面α内，直线b在平面β内，且a、b与l均不垂直，则（ ）
| A． | a与b可能垂直，但不可能平行 | B． | a与b可能垂直也可能平行 | ||
| C． | a与b不可能垂直，但可能平行 | D． | a与b不可能垂直，也不可能平行 |
3．已知P是以F1，F2为焦点的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的一点，若PF1⊥PF2，且|PF1|=2|PF2|，则此椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{5}}{3}$ |
4．
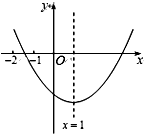已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列结论中：
①b2-4ac＞0；
②abc＞0；
③b=-2a；
④9a+3b+c＜0，
正确结论的个数是（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列结论中：①b2-4ac＞0；
②abc＞0；
③b=-2a；
④9a+3b+c＜0，
正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
5．已知双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{3}{4}$x，且其右焦点为（5，0），则双曲线C的方程为（ ）
| A． | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | C． | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |