题目内容
已知动点P与双曲线 -
- =1的两个焦点F1、F2的距离之和为定值,且cos∠F1PF2的最小值为-
=1的两个焦点F1、F2的距离之和为定值,且cos∠F1PF2的最小值为- ,则动点P的轨迹方程为 .
,则动点P的轨迹方程为 .
【答案】分析:根据椭圆定义可知,所求动点P的轨迹为以F1,F2为焦点的椭圆,再结合余弦定理求出椭圆中的a,b的值即可
解答:解:∵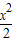 -
-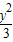 =1,∴c=
=1,∴c=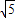 .
.
设|PF1|+|PF2|=2a(常数a>0),2a>2c=2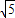 ,
,
∴a>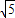 ,
,
设|PF1|=m,|PF2|=n,
由余弦定理有cos∠F1PF2
=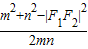 =
=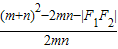 =
=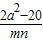 -1
-1
∵mn≤(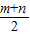 )2=a2,
)2=a2,
∴当且仅当m=n时,mn取得最大值a2.
此时cos∠F1PF2取得最小值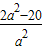 -1,
-1,
由题意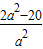 -1=-
-1=- ,
,
解得a2=18,
∴b2=a2-c2=18-5=13
∴P点的轨迹方程为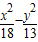 =1.
=1.
故答案为: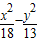 =1.
=1.
点评:本题考查了圆锥曲线的轨迹问题,考查椭圆的定义与椭圆的标准方程,考查余弦定理与基本不等式求最值.本题是圆锥曲线与基本不等式知识的一个综合题,知识覆盖面较广.
解答:解:∵
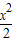 -
-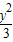 =1,∴c=
=1,∴c=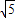 .
.设|PF1|+|PF2|=2a(常数a>0),2a>2c=2
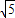 ,
,∴a>
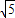 ,
,设|PF1|=m,|PF2|=n,
由余弦定理有cos∠F1PF2
=
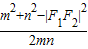 =
=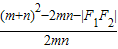 =
=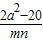 -1
-1∵mn≤(
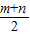 )2=a2,
)2=a2,∴当且仅当m=n时,mn取得最大值a2.
此时cos∠F1PF2取得最小值
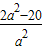 -1,
-1,由题意
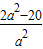 -1=-
-1=- ,
,解得a2=18,
∴b2=a2-c2=18-5=13
∴P点的轨迹方程为
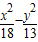 =1.
=1.故答案为:
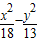 =1.
=1.点评:本题考查了圆锥曲线的轨迹问题,考查椭圆的定义与椭圆的标准方程,考查余弦定理与基本不等式求最值.本题是圆锥曲线与基本不等式知识的一个综合题,知识覆盖面较广.

练习册系列答案
相关题目