题目内容
设Sn是等比数列{an}的前n项和,且S3=
,S6=
.
(1)求{an}的通项公式an;
(2)设bn=log2an,求数列{bn}的前n项和Tn.
| 7 |
| 4 |
| 63 |
| 4 |
(1)求{an}的通项公式an;
(2)设bn=log2an,求数列{bn}的前n项和Tn.
分析:(1)设{an}的首项为a1,公比为q,分q=1与q≠1讨论,列方程组计算即可求得q,从而可求{an}的通项公式an;
(2)由an=2n-3,bn=log2an,可求得bn=n-3,从而可求得b1,利用等差数列的前n项和公式即可求得Tn.
(2)由an=2n-3,bn=log2an,可求得bn=n-3,从而可求得b1,利用等差数列的前n项和公式即可求得Tn.
解答:解:(1)设{an}的首项为a1,公比为q
当q=1时,S3=3a1,S6=6a1,则S6=2S3,不合题意; …(2分)
当q≠1时,
,两式相除得1+q3=9,
∴q=2,
∴a1=
…(6分)
∴an=a1qn-1=
×2n-1=2n-3…(8分)
(2)bn=log2an=log22n-3=n-3,…11分
∴b1=-2,
∴Tn=
=
=
…14分
当q=1时,S3=3a1,S6=6a1,则S6=2S3,不合题意; …(2分)
当q≠1时,
|
∴q=2,
∴a1=
| 1 |
| 4 |
∴an=a1qn-1=
| 1 |
| 4 |
(2)bn=log2an=log22n-3=n-3,…11分
∴b1=-2,
∴Tn=
| n(b1+bn) |
| 2 |
| n(-2+n-3) |
| 2 |
| n(n-5) |
| 2 |
点评:本题考查数列的求和,突出考查等比数列与等差数列的通项公式及求和公式,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
设Sn是等比数列{an}的前n项和,
=
,则
等于( )
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 的前n项和,若
的前n项和,若 ,则
,则 ( )
( )  B、
B、 C、
C、 D、
D、
 ,则
,则 等于( )
等于( )



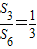 ,则
,则 等于( )
等于( )


