题目内容
15.设$\overrightarrow{a}$=(-2,-3),$\overrightarrow{b}$=(6,-5).则$\overrightarrow{a}$$•\overrightarrow{b}$=3.分析 根据题意,由向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标,将其代入向量的数量积坐标计算公式计算可得答案.
解答 解:根据题意,$\overrightarrow{a}$=(-2,-3),$\overrightarrow{b}$=(6,-5),
则$\overrightarrow{a}$$•\overrightarrow{b}$=(-2)×6+(-3)×(-5)=3;
即$\overrightarrow{a}$$•\overrightarrow{b}$=3;
故答案为:3.
点评 本题考查平面向量数量积的坐标运算,关键是熟练掌握平面向量数量积的坐标运算公式并灵活运用.

练习册系列答案
相关题目
5.数列{an}满足:an+1=λan-1(n∈N*,λ∈R且λ≠0),若数列{an-1}是等比数列,则λ的值等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
3.用1,2,3,4四个数字组成一个四位数,其中大于3300的偶数有多少个( )
| A. | 128 | B. | 64 | C. | 96 | D. | 48 |
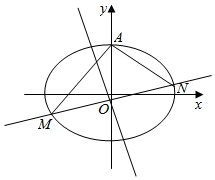 已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$
已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$