题目内容
9.设函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x},x>1}\\{-x-2,x≤1}\end{array}\right.$,则函数f(x)的值域是(0,1)∪[-3,+∞).分析 可根据不等式的性质,根据x的范围,可以分别求出$\frac{1}{x}$和-x-2的范围,从而求出f(x)的值域.
解答 解:①x>1时,f(x)=$\frac{1}{x}$;
∴$0<\frac{1}{x}<1$;
即0<f(x)<1;
②x≤1时,f(x)=-x-2;
∴-x≥-1;
∴-x-2≥-3;
即f(x)≥-3;
∴函数f(x)的值域为(0,1)∪[-3,+∞).
故答案为:(0,1)∪[-3,+∞).
点评 考查函数值域的概念,分段函数值域的概念,以及根据不等式的性质求函数值域的方法.

练习册系列答案
相关题目
17.某市高三文科共有2000人参加数学调研测试,为了解本次调研成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为150分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
(2)估计该市文科调研测试的平均分数(同一组中的数据用该区间的中点值作代表);
(3)用分层抽样的方法在分数段[50,70),[130,150)的学生中抽取一个容量为4的样本,将该样本看成一个总体,从中任取2人,求2人都在分数段[50,70)的概率.
| 分组 | 频数 | 频率 |
| 50~70 | 30 | 0.06 |
| 70~90 | 0.42 | |
| 90~110 | 190 | |
| 110~130 | 60 | 0.12 |
| 130~150 | ||
| 合计 | 500 | 1.00 |
(2)估计该市文科调研测试的平均分数(同一组中的数据用该区间的中点值作代表);
(3)用分层抽样的方法在分数段[50,70),[130,150)的学生中抽取一个容量为4的样本,将该样本看成一个总体,从中任取2人,求2人都在分数段[50,70)的概率.
1.将函数y=sinx的图象向左平移$\frac{π}{12}$个单位,然后将图象所有点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),则所得函数解析式为( )
| A. | $y=sin(\frac{1}{2}x+\frac{π}{12})$ | B. | $y=sin(\frac{1}{2}x-\frac{π}{12})$ | C. | $y=sin(2x+\frac{π}{12})$ | D. | $y=sin(2x-\frac{π}{6})$ |
18.某班一次数学考试后的成绩如表所示:
据此估计,该班本次数学测试的平均成绩为82.
| 成绩分组 | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 5 | 15 | 20 | 10 |
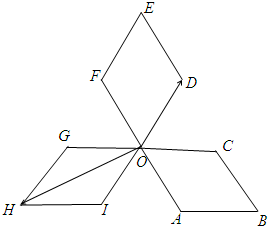 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )