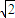题目内容
若F1、F2为双曲线C: 的左、右焦点,O为坐标原点,点P及N (2,
的左、右焦点,O为坐标原点,点P及N (2, )均在双曲线上,M在C的右准线上,且满足
)均在双曲线上,M在C的右准线上,且满足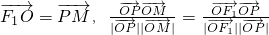 .
.
(1)求双曲线C的离心率及其方程;
(2)设双曲线C的虚轴端点B1、B2(B1在y轴的正半轴上),点A,B在双曲线上,且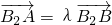 ,当
,当 时,求直线AB的方程.
时,求直线AB的方程.
解:(1)由题知:|OF1|=|PM|=c,∠F1OP=∠POM,∴F1OMP是菱形,…(1分)
∵由双曲线第一定义:|PF2|-|PF1|=2a,|PF1|=|OF1|=c,
∴|PF2|=2a+c,
∴由双曲线第二定义得:e=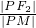 =
= ;
;
∴e=2 +1,即e2-e-2=0;
+1,即e2-e-2=0;
解得e=2或e=-1(舍);…(3分)
∵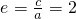 ,∴c=2a,
,∴c=2a,
∴b2=3a2
将N(2, )代入双曲线方程得
)代入双曲线方程得 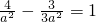 ,
,
∴a2=3,b2=9…(5分)
∴所求双曲线方程为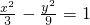 …(6分)
…(6分)
(2)由(1)知B1(0,3),B2(0,-3),
∵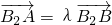 ,∴B2,A,B三点共线,即直线AB过B2(0,-3),
,∴B2,A,B三点共线,即直线AB过B2(0,-3),
∴设A(x1,y1),B(x2,y2),则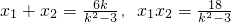 .
.
∵ ,
,
∴x1x2+y1y2-3(y1+y2)+9=0,
∴(1+k2)x1x2-6k(x1+x2)+36=0.
将x1+x2和x1x2代入,得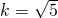 .
.
检验满足△>0,
∴直线AB的方程为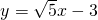 .
.
分析:(1)由题知:|OF1|=|PM|=c,∠F1OP=∠POM,故F1OMP是菱形,由双曲线第一定义:|PF2|-|PF1|=2a,|PF1|=|OF1|=c,故|PF2|=2a+c,由双曲线第二定义得:e=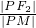 =
= ,解得e=2或e=-1(舍),由此能求出双曲线方程.
,解得e=2或e=-1(舍),由此能求出双曲线方程.
(2)由(1)知B1(0,3),B2(0,-3),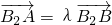 ,故直线AB过B2(0,-3),设A(x1,y1),B(x2,y2),则
,故直线AB过B2(0,-3),设A(x1,y1),B(x2,y2),则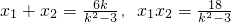 .由
.由 ,知(1+k2)x1x2-6k(x1+x2)+36=0.由此能求出直线AB的方程.
,知(1+k2)x1x2-6k(x1+x2)+36=0.由此能求出直线AB的方程.
点评:本题考查双曲线C的离心率及其方程的求法,求直线AB的方程.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
∵由双曲线第一定义:|PF2|-|PF1|=2a,|PF1|=|OF1|=c,
∴|PF2|=2a+c,
∴由双曲线第二定义得:e=
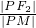 =
= ;
;∴e=2
 +1,即e2-e-2=0;
+1,即e2-e-2=0;解得e=2或e=-1(舍);…(3分)
∵
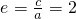 ,∴c=2a,
,∴c=2a,∴b2=3a2
将N(2,
 )代入双曲线方程得
)代入双曲线方程得 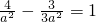 ,
,∴a2=3,b2=9…(5分)
∴所求双曲线方程为
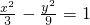 …(6分)
…(6分)(2)由(1)知B1(0,3),B2(0,-3),
∵
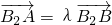 ,∴B2,A,B三点共线,即直线AB过B2(0,-3),
,∴B2,A,B三点共线,即直线AB过B2(0,-3),∴设A(x1,y1),B(x2,y2),则
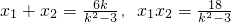 .
.∵
 ,
,∴x1x2+y1y2-3(y1+y2)+9=0,
∴(1+k2)x1x2-6k(x1+x2)+36=0.
将x1+x2和x1x2代入,得
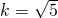 .
.检验满足△>0,
∴直线AB的方程为
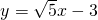 .
.分析:(1)由题知:|OF1|=|PM|=c,∠F1OP=∠POM,故F1OMP是菱形,由双曲线第一定义:|PF2|-|PF1|=2a,|PF1|=|OF1|=c,故|PF2|=2a+c,由双曲线第二定义得:e=
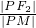 =
= ,解得e=2或e=-1(舍),由此能求出双曲线方程.
,解得e=2或e=-1(舍),由此能求出双曲线方程.(2)由(1)知B1(0,3),B2(0,-3),
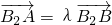 ,故直线AB过B2(0,-3),设A(x1,y1),B(x2,y2),则
,故直线AB过B2(0,-3),设A(x1,y1),B(x2,y2),则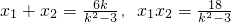 .由
.由 ,知(1+k2)x1x2-6k(x1+x2)+36=0.由此能求出直线AB的方程.
,知(1+k2)x1x2-6k(x1+x2)+36=0.由此能求出直线AB的方程.点评:本题考查双曲线C的离心率及其方程的求法,求直线AB的方程.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
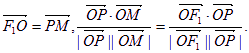 (Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点
(Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点 =
=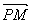 .
.
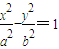 的左、右焦点,O为坐标原点,点P在双曲线的左支上,点M在双曲线的右准线上,且满足
的左、右焦点,O为坐标原点,点P在双曲线的左支上,点M在双曲线的右准线上,且满足 (λ>0),则该双曲线的离心率为( )
(λ>0),则该双曲线的离心率为( )