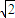题目内容

若F1、F2为双曲线
x2
a2
-
y2
b2
=1的左、右焦点，O为坐标原点，点P在双曲线的左支上，点M在双曲线的右准线上，且满足
F1O
=
PM
， 
OP
=λ(
OF1
|
OF
1|
+
OM
|
OM
|
)（λ＞0），则该双曲线的离心率为（　　）
A、
2
B、
3
C、2
D、3
分析：由
F1O
=
PM
， 
OP
=λ(
OF1
|
OF
1|
+
OM
|
OM
|
)可知F1OMP是菱形，由此可以导出a，b，c的数量关系，从而求出双曲线的离心率．
解答：解：∵
F1O
=
PM
， 
OP
=λ(
OF1
|
OF
1|
+
OM
|
OM
|
)，
∴四边形F1OMP是菱形，
设PM与y轴交于点N，
∵|F1O|=|PM|=c，MN=
a2
c
，
∴P点的横坐标为-(c-
a2
c
) =-
b2
c
，
把x=-
b2
c
代入双曲线
x2
a2
-
y2
b2
=1得
y=±
c4
a2
-
a4
c2
-4c2+4a2
，
∴M(
a2
c
，
c4
a2
-
a4
c2
-4c2+4a2)，
∴|OM|=
c4
a2
-4c2+4a2
．
∵四边形F1OMP是菱形，∴|OM|=|F1O|，
∴
c4
a2
-4c2+4a2
=c．
整理得e4-5e2+4=0，解得e2=4或e2=1（舍去）．
∴e=2，或e=-2（舍去）．
点评：能够判断出F1OMP是菱形，这是正确解题的关键步骤．
练习册系列答案
相关题目
若F1、F2为双曲线C：
x2
a2
-
y2
b2
=1的左、右焦点，O为坐标原点，点P及N （2，
3
）均在双曲线上，M在C的右准线上，且满足
F1O
=
PM
，
OP
•
OM
|
OP
|•|
OM
|
=
OF1
•
OP
|
OF1
|•|
OP
|
．
（1）求双曲线C的离心率及其方程；
（2）设双曲线C的虚轴端点B1、B2（B1在y轴的正半轴上），点A，B在双曲线上，且
B2A
=λ
B2B
，当
B1A
•
B1B
=0时，求直线AB的方程．

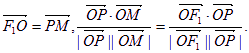(本题满分14分) 若F1、F2为双曲线的左、右焦点，O为坐标原点，P在双曲线左支上，M在右准线上，且满足（Ⅰ）求此双曲线的离心率；（Ⅱ）若此双曲线过点，求双曲线方程；（Ⅲ）设（Ⅱ）中双曲线的虚轴端点为B1，B2（B1在y轴正半轴上），求B2作直线AB与双曲线交于A、B两点，求时，直线AB的方程.
如图,若F1、F2为双曲线=1的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足=,

=.

(1)求双曲线的离心率;

(2)若双曲线过点N(2,),求双曲线的方程.

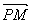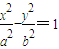若F1、F2为双曲线的左、右焦点，O为坐标原点，点P在双曲线的左支上，点M在双曲线的右准线上，且满足（λ＞0），则该双曲线的离心率为（ ）
A．
B．
C．2
D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网