题目内容
设a,b∈R,那么“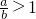 ”是“a>b>0”的
”是“a>b>0”的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
B
分析:a>b>0,可推出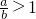 ,而当
,而当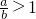 ,时,例如取a=-2,b=-1,显然不能推出a>b>0,由充要条件的定义可得答案.
,时,例如取a=-2,b=-1,显然不能推出a>b>0,由充要条件的定义可得答案.
解答:由不等式的性质,a>b>0,可推出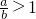 ,
,
而当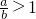 ,时,例如取a=-2,b=-1,显然不能推出a>b>0.
,时,例如取a=-2,b=-1,显然不能推出a>b>0.
故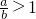 是a>b>0的必要不充分条件.
是a>b>0的必要不充分条件.
故选B.
点评:本题为充要条件的判断,正确利用不等式的性质是解决问题的关键,属基础题.
分析:a>b>0,可推出
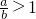 ,而当
,而当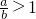 ,时,例如取a=-2,b=-1,显然不能推出a>b>0,由充要条件的定义可得答案.
,时,例如取a=-2,b=-1,显然不能推出a>b>0,由充要条件的定义可得答案.解答:由不等式的性质,a>b>0,可推出
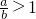 ,
,而当
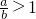 ,时,例如取a=-2,b=-1,显然不能推出a>b>0.
,时,例如取a=-2,b=-1,显然不能推出a>b>0.故
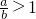 是a>b>0的必要不充分条件.
是a>b>0的必要不充分条件.故选B.
点评:本题为充要条件的判断,正确利用不等式的性质是解决问题的关键,属基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
设a,b∈R,那么“b(a-b)>0”是“a>b>0”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |