题目内容
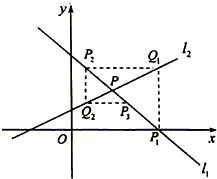 如图,直线l1:y=kx+1-k(k≠0,k≠±
如图,直线l1:y=kx+1-k(k≠0,k≠±| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)证明xn+1-1=
| 1 |
| 2k |
(Ⅱ)求数列{xn}的通项公式;
(Ⅲ)比较2|PPn|2与4k2|PP1|2+5的大小.
分析:(I)由题意及各点的产生情况直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn},读懂它即可得证;
(II)因为已知的直线l1方程且知直线l1与x轴交于点P1,可以求出点P1,在有(I)的证明结论可以得到数列{xn}的递推关系利用构造法求出其通项;
(III)先由题意得到点P的坐标为(1,1),在有两点间的距离的公式得2|PPn|2的式子,有式子与4k2|PP1|2+5比较大小.
(II)因为已知的直线l1方程且知直线l1与x轴交于点P1,可以求出点P1,在有(I)的证明结论可以得到数列{xn}的递推关系利用构造法求出其通项;
(III)先由题意得到点P的坐标为(1,1),在有两点间的距离的公式得2|PPn|2的式子,有式子与4k2|PP1|2+5比较大小.
解答:解:(Ⅰ)证明:设点Pn的坐标是(xn,yn),由已知条件得
点Qn、Pn+1的坐标分别是:(xn,
xn+
),(xn+1,
xn+
).
由Pn+1在直线l1上,得
xn+
=kxn+1+1-k.
所以
(xn-1)=k(xn+1-1),即xn+1-1=
(xn-1),n∈N*.
(Ⅱ)由题设知x1=1-
,x1-1=-
≠0,又由(Ⅰ)知xn+1-1=
(xn-1),
所以数列{xn-1}是首项为x1-1,公比为
的等比数列.
从而xn-1=-
×(
)n-1,即xn=1-2×(
)n,n∈N*.
(Ⅲ)解:由
得到点P的坐标为(1,1),
所以2|PPn|2=2(xn-1)2+2(kxn+1-k-1)2=8×(
)2n+2(
)2n-2,4k2|PP1|2+5=4k2[(1-
-1)2+(0-1)2]+5=4k2+9.
(i)当|k|>
,即k<-
或k>
时,4k2|PP1|2+5>1+9=10.
而此时0<|
|<1,所以2|PPn|2<8×1+2=10.故2|PPn|2<4k2|PP1|2+5.
(ii)当0<|k|<
,即k∈(-
,0)∪(0,
)时,4k2|PP1|2+5<1+9=10.
而此时|
|>1,所以2|PPn|2>8×1+2=10.故2|PPn|2>4k2|PP1|2+5.
点Qn、Pn+1的坐标分别是:(xn,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由Pn+1在直线l1上,得
| 1 |
| 2 |
| 1 |
| 2 |
所以
| 1 |
| 2 |
| 1 |
| 2k |
(Ⅱ)由题设知x1=1-
| 1 |
| k |
| 1 |
| k |
| 1 |
| 2k |
所以数列{xn-1}是首项为x1-1,公比为
| 1 |
| 2k |
从而xn-1=-
| 1 |
| k |
| 1 |
| 2k |
| 1 |
| 2k |
(Ⅲ)解:由
|
所以2|PPn|2=2(xn-1)2+2(kxn+1-k-1)2=8×(
| 1 |
| 2k |
| 1 |
| 2k |
| 1 |
| k |
(i)当|k|>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而此时0<|
| 1 |
| 2k |
(ii)当0<|k|<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而此时|
| 1 |
| 2k |
点评:此题重点考查了对于题意的准确理解,还考查了两点间的距离公式及构造法求数列的通项公式,此外还考查了比较含字母的式子的大小分类讨论的思想.

练习册系列答案
相关题目
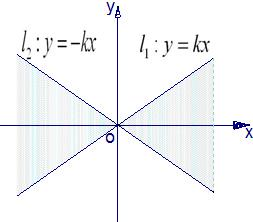 如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.

