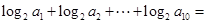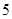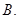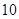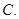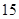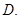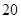题目内容
(本小题12分)设关于 的一元二次方程
的一元二次方程 有两根
有两根
 ,且满足
,且满足
(1)试用 表示
表示
(2)求证: 是等比数列
是等比数列
(3)当 时,求数列
时,求数列 的通项公式
的通项公式
 的一元二次方程
的一元二次方程 有两根
有两根 ,且满足
,且满足
(1)试用
 表示
表示
(2)求证:
 是等比数列
是等比数列(3)当
 时,求数列
时,求数列 的通项公式
的通项公式(1) ;(2)见解析;(3)
;(2)见解析;(3)
 ;(2)见解析;(3)
;(2)见解析;(3)
本试题主要是考查了根与系数的关系以及数列的定义和数列的通项公式的求解的综合运用。
(1)因为由题意结合韦达定理可知, 代入题设条件
代入题设条件
得 得到
得到 ,构造等比数列求解得到。
,构造等比数列求解得到。
(2)由于 ,故
,故
所以 是以
是以 为公比的等比数列
为公比的等比数列
(3)当 时,
时,
故数列 是以首项为
是以首项为 ,公比为
,公比为 的等比数列
的等比数列
从而得到表达式。
解:(1) 代入题设条件
代入题设条件
得
故
(2)由于 ,故
,故
所以 是以
是以 为公比的等比数列
为公比的等比数列
(3)当 时,
时,
故数列 是以首项为
是以首项为 ,公比为
,公比为 的等比数列
的等比数列

(1)因为由题意结合韦达定理可知,
 代入题设条件
代入题设条件
得
 得到
得到 ,构造等比数列求解得到。
,构造等比数列求解得到。(2)由于
 ,故
,故
所以
 是以
是以 为公比的等比数列
为公比的等比数列(3)当
 时,
时,
故数列
 是以首项为
是以首项为 ,公比为
,公比为 的等比数列
的等比数列从而得到表达式。
解:(1)
 代入题设条件
代入题设条件
得

故

(2)由于
 ,故
,故
所以
 是以
是以 为公比的等比数列
为公比的等比数列(3)当
 时,
时,
故数列
 是以首项为
是以首项为 ,公比为
,公比为 的等比数列
的等比数列

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
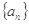 的前
的前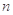 项和
项和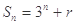 ,则
,则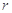 = ( )
= ( )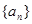 中,a1=3,前三项和为21,则a3 + a4 + a5 等于
中,a1=3,前三项和为21,则a3 + a4 + a5 等于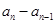 ,…是首项为1,公比为3的等比数列,则an等于( )
,…是首项为1,公比为3的等比数列,则an等于( )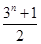
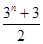
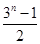
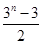
 为等比数列
为等比数列 ,
,
 有
有 ,求
,求 项和
项和
 }的首项及公比均为正数,令
}的首项及公比均为正数,令 ,若
,若 是数列{
是数列{ }的最小项,则k= 。
}的最小项,则k= 。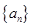 的各项均为正数,且
的各项均为正数,且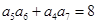 ,则
,则