题目内容
(本小题满分10分)选修4—1:几何证明选讲
如图所示,已知 为圆
为圆 的直径,
的直径, ,
, 是圆
是圆 上的两个点,
上的两个点, 于
于 ,
, 交
交 于
于 ,交
,交 于
于 ,
, .
.

(1)求证: 是劣弧
是劣弧 的中点;
的中点;
(2)求证: .
.
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)要证明 是劣弧
是劣弧 的中点,即证明弧
的中点,即证明弧 与弧
与弧 相等,即证明
相等,即证明 ,根据已知中
,根据已知中 ,
, 是圆
是圆 的直径,
的直径, 于
于 ,再根据同角的余角相等,得到结论;(2)由已知及(1)的结论,易正明
,再根据同角的余角相等,得到结论;(2)由已知及(1)的结论,易正明 及
及 均为等腰三角形,即
均为等腰三角形,即 ,
, ,进而得到结论.
,进而得到结论.
试题解析:(1)∵ ,∴
,∴ ,∵
,∵ 圆
圆 的直径,
的直径,
∴ ,∵
,∵ ,∴
,∴ ,
,
∵ ,
, ,∴
,∴ ,
,
∵ ,
, ,∴
,∴ ,
,
∴ ,∴
,∴ 为劣弧
为劣弧 的中点; 5分
的中点; 5分
(2)∵ ,
, ,
,
∴ ,∴
,∴ ,∴
,∴ . 10分
. 10分
考点:1.圆周角定理及其推论;2.同(等)角的余角相等.
考点分析: 考点1:圆的切线的性质及判定定理 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的最小值为 .
的最小值为 . 是定义在R上且周期为3的函数,当
是定义在R上且周期为3的函数,当  时,
时,  ,则方程
,则方程 在[-3,4]解的个数( )
在[-3,4]解的个数( ) ,且两条曲线在第一象限的交点为P,
,且两条曲线在第一象限的交点为P, 是以
是以  为底边的等腰三角形,若
为底边的等腰三角形,若  ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为  ,则
,则  的取值范围是( )
的取值范围是( ) B.
B.
 D.
D. ]
]
 的定义域是( )
的定义域是( ) B.
B.
 D.
D.
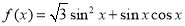 .
.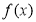 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;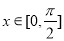 时,求函数
时,求函数 的值域.
的值域. 中,
中, ,
, ,
, ,
, ,
, 为
为 的三等分点,则
的三等分点,则 ( )
( ) B.
B. C.
C. D.
D.
 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 时,求函数
时,求函数 的值域.
的值域. 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 是
是 的中点,
的中点, 是
是 与
与 的交点.
的交点.
 平面
平面 ;
; 平面
平面 .
.