题目内容
已知  是定义在R上且周期为3的函数,当
是定义在R上且周期为3的函数,当  时,
时,  ,则方程
,则方程 在[-3,4]解的个数( )
在[-3,4]解的个数( )
A.4 B.8 C.9 D.10x
D
【解析】
试题分析:在同一坐标系中画出函数f(x)与 的图象,利用数形结合可得方程
的图象,利用数形结合可得方程 在[-3,4]解的个数.由题意知,f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|2x2-4x+1|,在同一坐标系中画出函数f(x)与
在[-3,4]解的个数.由题意知,f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|2x2-4x+1|,在同一坐标系中画出函数f(x)与 的图象如下图:
的图象如下图:
由图象可知:函数y=f(x)与 在区间[-3,4]上有10个交点(互不相同),所以方程
在区间[-3,4]上有10个交点(互不相同),所以方程 在[-3,4]解的个数是10个,故选:D.
在[-3,4]解的个数是10个,故选:D.

考点:二次函数的性质,函数周期性,根的存在性及个数判断
考点分析: 考点1:函数与方程 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
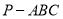 中,
中,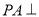 平面
平面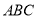 ,
,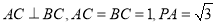 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )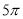 B.
B.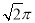 C.
C.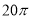 D.
D.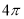
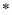 ”:
”: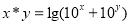 ,
,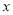 、
、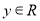 。对于任意实数
。对于任意实数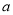 、
、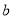 、
、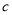 ,给出如下结论:①
,给出如下结论:①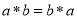 ;②
;②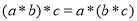 ;③
;③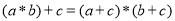 .其中正确结论的个数是 ( )
.其中正确结论的个数是 ( )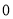 个 B.
个 B.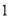 个 C.
个 C.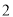 个 D.
个 D.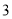 个
个 、
、 、
、 、
、 的四个小球,从盒子里随机摸出两个小球,那么事件“摸出的小球上标有的数字之和为
的四个小球,从盒子里随机摸出两个小球,那么事件“摸出的小球上标有的数字之和为 ”的概率是 .
”的概率是 . ,
, 对任意的实数x成立,则称f(x)是回旋函数.
对任意的实数x成立,则称f(x)是回旋函数. 为回旋函数,则t>l;
为回旋函数,则t>l; 不是回旋函数;
不是回旋函数; 的解集为( )
的解集为( )
 D.
D.
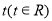 ,
,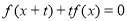 对任意的实数x成立,则称f(x)是回旋函数.
对任意的实数x成立,则称f(x)是回旋函数.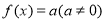 为回旋函数的充要条
为回旋函数的充要条 件是t= -1;
件是t= -1;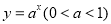 为回旋函数,则t>l;
为回旋函数,则t>l;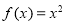 不是回
不是回 旋函数;
旋函数; 为圆
为圆 的直径,
的直径, ,
, 是圆
是圆 上的两个点,
上的两个点, 于
于 ,
, 交
交 于
于 ,交
,交 于
于 ,
, .
.
 是劣弧
是劣弧 的中点;
的中点; .
. 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D.