题目内容
7.已知数列{an}满足a1=$\frac{3}{8}$,若$\frac{{a}_{n+6}-{a}_{n}}{91}$≥3n≥an+2-an,则a2017=$\frac{1}{8}$•32017.分析 利用叠加法,结合条件得出an+6-an=91•3n,an+2-an=3n,进一步可得数列{an-$\frac{1}{8}$•3n}的奇数项是各项均为0的常数数列,即可得出结论.
解答 解:∵3n≥an+2-an,①
3n+2≥an+4-an+2,②
3n+4≥an+6-an+4,③
①+②+③:an+6-an≤3n+3n+2+3n+4=(1+32+34)•3n=91•3n,
又$\frac{{a}_{n+6}-{a}_{n}}{91}$≥3n,因此只有an+6-an=91•3n,
∴an+2-an=3n,
∴an+2-$\frac{1}{8}$•3n+2=an-$\frac{1}{8}$•3n,
∵a1=$\frac{3}{8}$,
∴a1-$\frac{1}{8}$•3=0
∴数列{an-$\frac{1}{8}$•3n}的奇数项是各项均为0的常数数列.
n为奇数时,an=$\frac{1}{8}$•3n,∴a2017=$\frac{1}{8}$•32017.
故答案为:$\frac{1}{8}$•32017.
点评 本题考查数列的通项,考查叠加法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
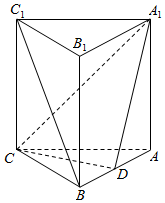 已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点
已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点